用1,2,3,4,5,6,7七個數字組成三個兩位數,一個一位數.已知這4個數的各個數位上的數字都不相同,并且4個數的和等于100.如果要求其中最大的兩位數盡可能大,那么這個最大的兩位數是多少?
【答案】分析:因為有三個兩位數,一個一位數,所以這7個數字里有3個數字做了十位數字,4個數字做了個位數字.不妨設這7個數字是a,b,c,d,e,f,g;其中a,b,c做了十位數字,d,e,f,g做了個位數字,先根據4個數的和等于100,得出10a+10b+10c+d+e+f+g=100,則d+e+f+g末尾一定是0,由于1+2+3+4+5+6+7=28,所以d+e+f+g=10或20.分兩種情況討論得出d+e+f+g只能等于20,再分情況討論可知,做十位數字的是5,2,1,做個位數字的是7,6,4,3,由此得出其中最大的兩位數.
解答:解:不妨設這7個數是a,b,c,d,e,f,g;其中a,b,c做了十位數字,d,e,f,g做了個位數字,
那么一定有10a+10b+10c+d+e+f+g=100,
所以d+e+f+g末尾一定是0.
∵1+2+3+4+5+6+7=28,∴d+e+f+g=10或20.
分兩種情況:
①當d+e+f+g=10時,
∵1+2+3+4=10,∴這時5,6,7做十位數字,
但是此時50+60+70+1+2+3+4=190≠100,不合題意,舍去;
②當d+e+f+g=20時,再分情況討論:
Ⅰ)假設用7做十位數字,
∵6+5+4+3=18<20,∴7只能做個位數字.
Ⅱ)假設用6做十位數字,
∵7+5+4+3=19<20,∴6也只能做個位數字.
Ⅲ)假設用5做十位數字,
∵7+6+4+3=20,∴此時做十位數字的是5,2,1.
又∵10(5+2+1)+7+6+4+3=100,滿足條件,
∴此時做十位數字的是5,2,1,做個位數字的是7,6,4,3.
∵要最大的兩位數,∴十位取5,個位取7,
故這個最大的兩位數是57.
點評:本題考查了數的十進制的有關知識及尾數特征,屬于競賽題型,有一定難度.運用分類討論思想是解決本題的關鍵.



 答下列問題:
答下列問題: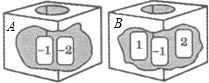 的卡片,它們分別寫有數字1,-1,2.現從A箱、B箱中各隨機地取出1張卡片,請你用畫樹形(狀)圖或列表的方法求:
的卡片,它們分別寫有數字1,-1,2.現從A箱、B箱中各隨機地取出1張卡片,請你用畫樹形(狀)圖或列表的方法求: