
【題目】如圖,已知AB∥CD,CE,BE的交點為E,現作如下操作:
第一次操作,分別作∠ABE和∠DCE的平分線,交點為E1,
第二次操作,分別作∠ABE1和∠DCE1的平分線,交點為E2,
第三次操作,分別作∠ABE2和∠DCE2的平分線,交點為E3……
第n次操作,分別作∠ABEn-1和∠DCEn-1的平分線,交點為En.
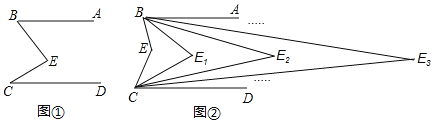
(1)如圖①,求證:∠E=∠B+∠C;
(2)如圖②,求證:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度數.
【答案】(1)證明見解析;(2)證明見解析;(3)∠BEC=2nb°.
【解析】試題分析:(1)先過E作EF∥AB,根據AB∥CD,得出AB∥EF∥CD,再根據平行線的性質,得出∠B=∠1,∠C=∠2,進而得到∠BEC=∠ABE+∠DCE;
(2)先根據∠ABE和∠DCE的平分線交點為E1,運用(1)中的結論,得出∠CE1B=∠ABE1+∠DCE1= ![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)根據∠ABE2和∠DCE2的平分線,交點為E3,得出∠BE3C=![]() ∠BEC;…據此得到規律∠En=
∠BEC;…據此得到規律∠En=![]() ∠BEC,最后求得∠BEC的度數.
∠BEC,最后求得∠BEC的度數.
試題解析:(1)如圖①,過E作EF∥AB,
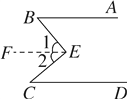
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如圖2,∵∠ABE和∠DCE的平分線交點為E1,

∴由(1)可得,
∠CE1B=∠ABE1+∠DCE1=![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;
∠BEC;
∵∠ABE1和∠DCE1的平分線交點為E2,
∴由(1)可得,
∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)如圖2,∵∠ABE2和∠DCE2的平分線,交點為E3,
∴∠BE3C=∠ABE3+∠DCE3=![]() ∠ABE2+
∠ABE2+![]() ∠DCE2=
∠DCE2=![]() ∠CE2B=
∠CE2B=![]() ∠BEC;
∠BEC;
…
以此類推,∠En=![]() ∠BEC,
∠BEC,
∴當∠En=α度時,∠BEC等于2nα度.


科目:初中數學 來源: 題型:
【題目】當m是何值時,關于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一個根,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是線段AB上一點,△ACD和△BCE都是等邊三角形,連結AE,BD,設AE交CD于點F.
(1)求證:△ACE≌△DCB;
(2)求證:△ADF∽△BAD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AD∥BC,∠1=∠2,要說明∠3+∠4=180°,請補充完整解題過程,并在括號內填上相應的依據:

解:因為AD∥BC(已知),
所以∠1=∠3( ).
因為∠1=∠2(已知),
所以∠2=∠3.
所以BE∥________( ).
所以∠3+∠4=180°( ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(
的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(![]() ,﹣2);⑤當x<
,﹣2);⑤當x<![]() 時,y隨x的增大而減小;⑥a+b+c>0正確的有( )
時,y隨x的增大而減小;⑥a+b+c>0正確的有( )

A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,CE平分∠ACD交AB于E點.
(1)求證:△ACE是等腰三角形;
(2)若AC=13cm,CE=24cm,求△ACE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠MON=α,點P是∠MON角平分線上一點,點A在射線OM上,作∠APB=180°-α,交直線ON于點B,PC⊥ON于C.
(1)如圖1,若∠MON=90°時,求證:PA=PB;
(2)如圖2,若∠MON=60°時,寫出線段OB,OA及BC之間的數量關系,并說明理由;
(3)如圖3,若∠MON=60°時,點B在射線ON的反向延長線上時,(2)中結論還成立嗎?若不成立,直接寫出線段OB,OA及BC之間的數量關系(不需要證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年5月的第二周為:“職業教育活動周”,今年我市展開了以“弘揚工匠精神,打造技能強國”為主題的系列活動,活動期間某職業中學組織全校師生并邀請學生家長和社區居民參加“職教體驗觀摩”活動,相關職業技術人員進行了現場演示,活動后該校隨機抽取了部分學生進行調查:“你最感興趣的一種職業技能是什么?”并對此進行了統計,繪制了統計圖(均不完整). 
(1)補全條形統計圖和扇形統計圖;
(2)若該校共有3000名學生,請估計該校對“工藝設計”最感興趣的學生有多少人?
(3)要從這些被調查的學生中隨機抽取一人進行訪談,那么正好抽到對“機電維修”最感興趣的學生的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,AB∥CD,分別探究下列四個圖形(圖①、②、③、④)中∠APC和∠PAB、∠PCD的數量關系,用等式表示出來.

(1)設∠APC=m,∠PAB=n,∠PCD=t.
請用含m,n,t的等式表示四個圖形中相應的∠APC和∠PAB、∠PCD的數量關系.(直接寫出結果)
圖①: ;
圖②: ;
圖③: ;
圖④: .
(2)在(1)中的4個結論中選出一個你喜歡的結論加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com