【題目】在平面直角坐標系中，△ABC的位置如圖所示（每個小方格都是邊長為1個單位長度的正方形）．其中A（1，1）、B（4，4）、C（5，1）．
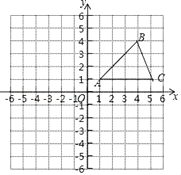
（1）將△ABC沿x軸方向向左平移6個單位，畫出平移后得到的△A1B1C1；
（2）將△ABC繞著點A順時針旋轉90°，畫出旋轉后得到的△A2B2C2，A、B、C的對應點分別是A2、B2、C2；
（3）連CB2，直接寫出點B2、C2的坐標B2： 、C2： ．
寒假樂園北京教育出版社系列答案科目：初中數學 來源： 題型：
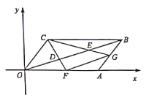
【題目】在平面直角坐標系中，平行四邊形
的頂點
的坐標分別是
,
,點
把線段
三等分，延長
分別交
于點
,連接
, 則下列結論:
; 
③四邊形
的面積為
;④
,其中正確的有（ ）.
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線
和直線外三點
，按下列要求畫圖，填空：
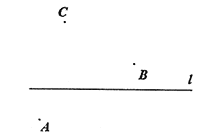
（1）畫射線
；
（2）連接
；
（3）延長
至
，使得
；
（4）在直線上確定點
，使得
最小，請寫出你作圖的依據___________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（14分）如圖，在平面直角坐標系中，拋物線y=mx2﹣8mx+4m+2（m＞2）與y軸的交點為A，與x軸的交點分別為B（x1，0），C（x2，0），且x2﹣x1=4，直線AD∥x軸，在x軸上有一動點E（t，0）過點E作平行于y軸的直線l與拋物線、直線AD的交點分別為P、Q．
（1）求拋物線的解析式；
（2）當0＜t≤8時，求△APC面積的最大值；
（3）當t＞2時，是否存在點P，使以A、P、Q為頂點的三角形與△AOB相似？若存在，求出此時t的值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們學過角的平分線的概念．類比給出新概念：從一個角的頂點出發，把這個角分成
的兩個角的射線，叫做這個角的三分線．顯然，一個角的三分線有兩條，例如：如圖1，若
，則
是
的一條三分線．
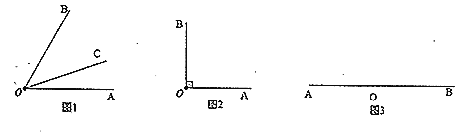
（1）如圖1，若
，若
，求
的度數；
（2）如圖2，若
，若
是的兩條三分線．
①求
的度數；
②現以O為中心，將順時針旋轉
度（
）得到
，當
恰好是的三分線時，則求的值．
（3）如圖3，若
，是的一條三分線，
分別是與
的平分線，將
繞點
以每秒
的速度沿順時針方向旋轉一周，在旋轉的過程中，若射線
恰好是的三分線，則此時繞點旋轉的時間是多少秒？（直接寫出答案即可，不必說明理由）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖①②③是三張形狀、大小完全相同的方格紙，方格紙中的每個小正方形的邊長均為1，每個小正方形的頂點叫做格點．
（1）圖①中△MON的面積=________；
（2）在圖②③中以格點為頂點畫出一個正方形ABCD，使正方形ABCD的面積等于（1）中△MON面積的4倍，并將正方形ABCD分割成以格點為頂點的四個全等的直角三角形和一個正方形，且正方形ABCD的面積沒有剩余（在圖②、圖③中畫出的圖形不能是全等形）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算與合并同類項：
(1)+4.7+(﹣4)﹣2.7﹣(﹣3.5)
(2)11÷(﹣22)﹣3×(﹣11)
(3)16+(﹣2)3+|﹣7|+(
)×(﹣4)
(4)0.25×(﹣2)2﹣[﹣4÷(
)2+1]÷(﹣1)2020
(5)5x4+3x2y﹣10﹣3x2y+x4﹣1
(6)(7y﹣3z)﹣(8y﹣5z)
(7)2(2a2+9b)+3(﹣5a2﹣6b)
(8)﹣3(2x2﹣xy)﹣4(x2﹣xy﹣6)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有個填寫運算符號的游戲：在“
”中的每個□內，填入
中的某一個（可重復使用），然后計算結果．
（1）計算：
；
（2）若請推算
□內的符號；
（3）在“
”的□內填入符號后，使計算所得數最小，直接寫出這個最小數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
