
如圖,正方形ABCD的邊CD在正方形ECGF的邊CE上,O是EG的中點,∠EGC的平分線GH過點D,交BE于點H,連接OH,FH,EG與FH交于點M,對于下面四個結論:①CH⊥BE;②HO
 BG;③S正方形ABCD:S正方形ECGF=1:
BG;③S正方形ABCD:S正方形ECGF=1: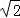 ;④EM:MG=1:(1+
;④EM:MG=1:(1+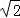 ),其中正確結論的序號為 .
),其中正確結論的序號為 .
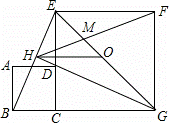
②解:∵四邊形ABCD是正方形,
∴BC=DC,∠BCE=90°,
同理可得CE=CG,∠DCG=90°,
在△BCE和△DCG中,
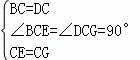 ,
,
∴△BCE≌△DCG,
∴∠BEC=∠DGC,
∵∠EDH=∠ CDG,∠DGC+∠CDG=90°,
CDG,∠DGC+∠CDG=90°,
∴∠EDH+∠BEC=90°,
∴∠EHD=90°,
∴HG⊥BE,則CH⊥BE錯誤,
則故①錯誤;
∵在△BGH和△EGH中,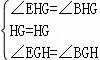 ,
,
∴△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中點,
∴HO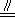
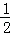 BG,
BG,
故②正確;
設EC和OH相交于點N.
設HN=a,則BC=2a,設正方形ECGF的邊長是2b,則NC=b,CD=2a,
∵OH∥BC,
∴△DHN∽△DGC,
∴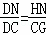 ,即
,即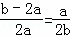 ,即a2+2ab﹣b2=0,
,即a2+2ab﹣b2=0,
解得:a=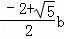 或a=
或a=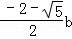 (舍去),
(舍去),
則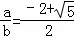 ,
,
則S正方形ABCD:S正方形ECGF=(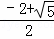 )2=
)2=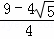 ,故③錯誤;
,故③錯誤;
∵EF∥OH,
∴△EFM∽△OMH,
∴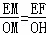 =
=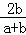 ,
,
∴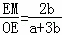 ,
,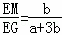
∴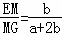 =
=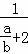 =
=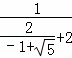 =
=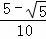 .故④錯誤.
.故④錯誤.
故正確的是②.
故答案是:②.


科目:初中數學 來源: 題型:
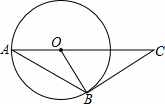
如圖,AB是⊙O的弦,AO的延長線交過點B的⊙O的切線于點C,如果∠ABO=20°,則∠C的度數是( )
|
| A. | 70° | B. | 50° | C. | 45° | D. | 20° |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,正方形ABCD位于第一象限,邊長為3,點A在直線y=x上,點A的橫坐標為1,正方形ABCD的邊分別平行于x軸、y軸.若雙曲線y= 與正方形ABCD有公共點,則k的取值范圍為( )
與正方形ABCD有公共點,則k的取值范圍為( )
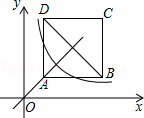
|
| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
查看答案和解析>>
科目:初中數學 來源: 題型:
為了掌握我市中考模擬數學試題的命題質量與難度系數,命題教師赴我市某地選取一個水平相當的初三年級進行調研,命題教師將隨機抽取的部分學生成績(得分為整數,滿分為160分)分為5組:第一組85~10;第二組100~115;第三組115~130;第四組130~145;第五組145~160,統計后得到如圖所示的頻數分布直方圖(每組含最小值不含最大值)和扇形統計圖,觀察圖形的信息,回答下列問題:
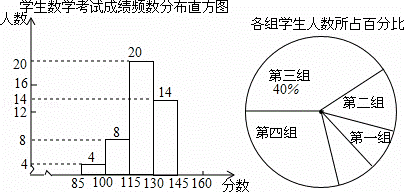
(1)本次調查共隨機抽取了該年級多少名學生?并將頻數分布直方圖補充完整;
(2)若將得分轉化為等級,規定:得分低于100分評為“D”,100~130分評為“C”,130~145分評為“B”,145~160分評為“A”,那么該年級1500名考生中,考試成績評為“B”的學生大約有多少名?
(3)如果第一組只有一名是女生,第五組只有一名是男生,針對考試成績情況,命題教師決定從第一組、第五組分別隨機選出一名同學談談做題的感想,請你用列表或畫樹狀圖的方法求出所選兩名學生剛好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
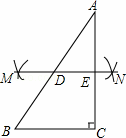
已知在Rt△ABC中,∠ACB=90°,現按如下步驟作圖:
①分別以A,C為圓心,a為半徑(a>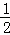 AC)作弧,兩弧分別交于M,N兩點;
AC)作弧,兩弧分別交于M,N兩點;
②過M,N兩點作直線MN交AB于點D,交AC于點E;
③將△ADE繞點E順時針旋轉180°,設點D的像為點F.
(1)請在圖中直線標出點F并連接CF;
(2)求證:四邊形BCFD是平行四邊形;
(3)當∠B為多少度時,四邊形BCFD是菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com