解:(1)∵AB的垂直平分線為y軸,
∴OA=OB=

AB=

×2=1,
∴A的坐標是(-1,0),B的坐標是(1,0).
在直角△OAC中,OC=

=2,
則C的坐標是:(0,2);
(2)設拋物線的解析式是:y=ax
2+b,
根據題意得:
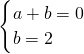
,
解得:

,
則拋物線的解析式是:y=-2x
2+2;
(3)∵S
△ABC=

AB•OC=

×2×2=2,
∴S
△ABD=

S
△ABC=1.
設D的縱坐標是m,則

AB•|m|=1,
則m=±1.
當m=1時,-2x
2+2=1,解得:x=±

,
當m=-1時,-2x
2+2=-1,解得:x=±

,
則D的坐標是:(

,1)或(-

,1)或(

,-1),或(-

,-1).
(4)設拋物線向右平移c個單位長度,則0<c≤1,OA′=1-c,OB′=1+c.
平移以后的拋物線的解析式是:y=-2(x-c)
2+b.
令x=0,解得y=-2c
2+2.即OC′=-2c
2+2.
當點C′同時在以A′B′為直徑的圓上時有:OC′
2=OA′•OB′,
則(-2c
2+2)
2=(1-c)(1+c),
即(4c
2-3)(c
2-1)=0,
解得:c=

,-

(舍去),1,-1(舍去).
故平移

或1個單位長度.
分析:(1)根據y軸是AB的垂直平分線,則可以求得OA,OB的長度,在直角△OAC中,利用勾股定理求得OC的長度,則A、B、C的坐標即可求解;
(2)利用待定系數法即可求得二次函數的解析式;
(3)首先求得△ABC的面積,根據S
△ABD=

S
△ABC,以及三角形的面積公式,即可求得D的縱坐標,把D的縱坐標代入二次函數的解析式,即可求得橫坐標.
(4)設拋物線向右平移c個單位長度,則0<c≤1,可以寫出平移以后的函數解析式,當點C′同時在以A′B′為直徑的圓上時有:OC′
2=OA′•OB′,據此即可得到一個關于c的方程求得c的值.
點評:本題考查了勾股定理,待定系數法求二次函數的解析式,以及圖象的平移,正確理解:當點C′同時在以A′B′為直徑的圓上時有:OC′
2=OA•OB,是解題的關鍵.

 如圖,在△ABC中,AB=2,AC=BC=
如圖,在△ABC中,AB=2,AC=BC= .
. S△ABC;
S△ABC; ,y4=-
,y4=- .
. ,y4=-
,y4=- .
. ,可設y=
,可設y= ,用同樣的方法也可求解.
,用同樣的方法也可求解. AB=
AB= ×2=1,
×2=1, =2,
=2,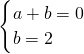 ,
, ,
, AB•OC=
AB•OC= ×2×2=2,
×2×2=2, S△ABC=1.
S△ABC=1. AB•|m|=1,
AB•|m|=1, ,
, ,
, ,1)或(-
,1)或(- ,1)或(
,1)或( ,-1),或(-
,-1),或(- ,-1).
,-1). ,-
,- (舍去),1,-1(舍去).
(舍去),1,-1(舍去). 或1個單位長度.
或1個單位長度. S△ABC,以及三角形的面積公式,即可求得D的縱坐標,把D的縱坐標代入二次函數的解析式,即可求得橫坐標.
S△ABC,以及三角形的面積公式,即可求得D的縱坐標,把D的縱坐標代入二次函數的解析式,即可求得橫坐標.

 如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為
如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為