
如圖,在直角坐標系中,矩形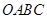 的頂點
的頂點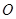 與坐標原點重合,頂點
與坐標原點重合,頂點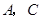 在坐標軸上,
在坐標軸上,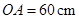 ,
,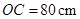 .動點
.動點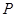 從點
從點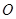 出發,以
出發,以 的速度沿
的速度沿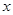 軸勻速向點
軸勻速向點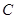 運動,到達點
運動,到達點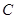 即停止.設點
即停止.設點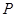 運動的時間為
運動的時間為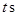 .
.
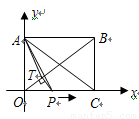
(1)過點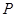 作對角線
作對角線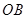 的垂線,垂足為點
的垂線,垂足為點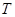 .求
.求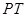 的長
的長 與時間
與時間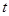 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量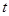 的取值范圍;
的取值范圍;
(2)在點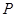 運動過程中,當點
運動過程中,當點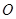 關于直線
關于直線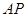 的對稱點
的對稱點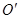 恰好落在對角線
恰好落在對角線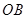 上時,求此時直線
上時,求此時直線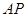 的函數解析式;
的函數解析式;
(3)探索:以 三點為頂點的
三點為頂點的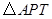 的面積能否達到矩形
的面積能否達到矩形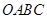 面積的
面積的 ?請說明理由.
?請說明理由.
(1)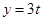 ,
,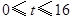 (2)
(2)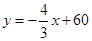 (3)不能,理由見解析
(3)不能,理由見解析
【解析】解:(1)在矩形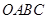 中,
中,
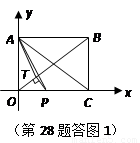
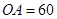 ,
,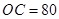 ,
,
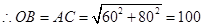 .……………………1分
.……………………1分
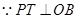 ,
,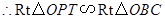 .
.
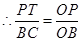 ,即
,即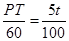 ,
,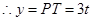 .……3分
.……3分
當點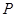 運動到
運動到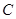 點時即停止運動,此時
點時即停止運動,此時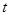 的最大值為
的最大值為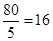 .
.
所以,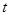 的取值范圍是
的取值范圍是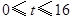 .················ 4分
.················ 4分
(2)當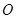 點關于直線
點關于直線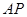 的對稱點
的對稱點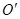 恰好在對角線
恰好在對角線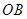 上時,
上時,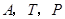 三點應在一條直線上(如答圖2).……………………5分
三點應在一條直線上(如答圖2).……………………5分
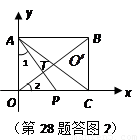
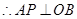 ,
,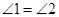 .
.
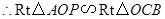 ,
,
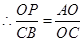 .
.
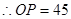 .
.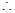 點
點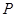 的坐標為
的坐標為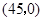 .…………6分
.…………6分
設直線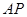 的函數解析式為
的函數解析式為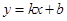 .將點
.將點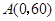 和點
和點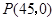 代入解析式,得
代入解析式,得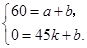 解這個方程組,得
解這個方程組,得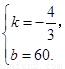
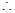 此時直線
此時直線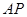 的函數解析式是
的函數解析式是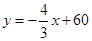 .········· 8分
.········· 8分
(3)由(2)知,當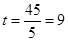 時,
時,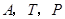 三點在一條直線上,此時點
三點在一條直線上,此時點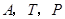 不構成三角形.
不構成三角形.
故分兩種情況:
(i)當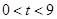 時,點
時,點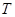 位于
位于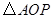 的內部(如答圖3).
的內部(如答圖3).
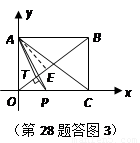
過 點作
點作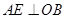 ,垂足為點
,垂足為點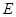 ,由
,由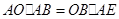
可得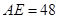 .
.
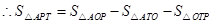
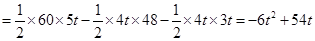 .······· 10分
.······· 10分
若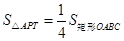 ,則應有
,則應有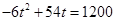 ,即
,即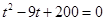 .
.
此時,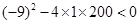 ,所以該方程無實數根.
,所以該方程無實數根.
所以,當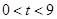 時,以
時,以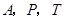 為頂點的
為頂點的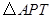 的面積不能達到矩形
的面積不能達到矩形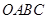 面積的
面積的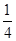 . 11分
. 11分
(ii)當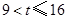 時,點
時,點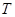 位于
位于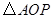 的外部.(如答圖4)
的外部.(如答圖4)
此時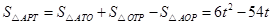 .········ 12分
.········ 12分
若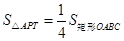 ,則應有
,則應有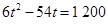 ,即
,即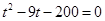 .
.
解這個方程,得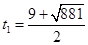 ,
,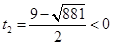 (舍去).
(舍去).
由于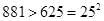 ,
,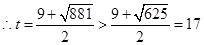 .
.
而此時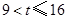 ,所以
,所以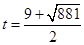 也不符合題意,故舍去.
也不符合題意,故舍去.
所以,當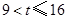 時,以
時,以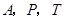 為頂點的
為頂點的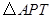 的面積也不能達到矩形
的面積也不能達到矩形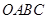 面積的
面積的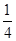 .
.
綜上所述,以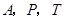 為頂點的
為頂點的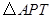 的面積不能達到矩形
的面積不能達到矩形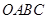 面積的
面積的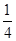 .
.
(1)找出三角形相似的條件,利用相似三角形的對應邊成比例,求出邊界值即可
(2)用待定系數法,找出直線上兩點坐標即可,由于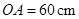 ,則
,則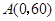 ,利用相似三角形的對應邊成比例,求出點P的坐標
,利用相似三角形的對應邊成比例,求出點P的坐標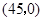
(3)由于點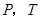 是動點,以
是動點,以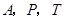 為頂點的
為頂點的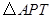 的面積與點
的面積與點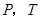 的位置有關,需分情況討論,當
的位置有關,需分情況討論,當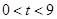 時,找不到
時,找不到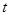 的值使得
的值使得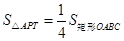 ,當
,當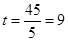 時,
時,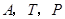 三點在一條直線上,則點
三點在一條直線上,則點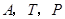 不構成三角形,當
不構成三角形,當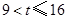 時,也找不到
時,也找不到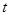 的值使得
的值使得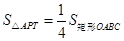 ,因此以
,因此以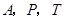 為頂點的
為頂點的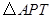 的面積不能達到矩形
的面積不能達到矩形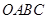 面積的
面積的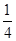


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′.
如圖,在直角坐標系中,點P的坐標為(3,4),將OP繞原點O逆時針旋轉90°得到線段OP′. | PP′ |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中數學 來源: 題型:
 ,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件:
,2).畫出△ABC的兩個位似圖形△A1B1C1,△A2B2C2,同時滿足下列兩個條件:查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com