
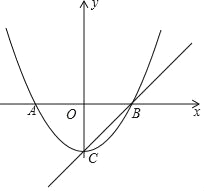
【題目】如圖,已知頂點為C(0,﹣3)的拋物線y=ax2+b(a≠0)與x軸交于A,B兩點,直線y=x+m過頂點C和點B.
(I)求點B的坐標;
(Ⅱ)求二次函數y=ax2+b(a≠0)的解析式;
(Ⅲ)拋物線y=ax2+b(a≠0)上是否存在點M,使得∠MCB=15°?若存在,求出點M的坐標;若不存在,請說明理由.
【答案】(I)(3,0);(Ⅱ)y=![]() ;(Ⅲ)(3
;(Ⅲ)(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).
【解析】
(Ⅰ)根據點C(0,﹣3),直線y=x+m過點C和點B,可以求得直線的解析式,從而可以求得點B的坐標;
(Ⅱ)根據點B和點C的坐標可以求得二次函數的解析式;
(Ⅲ)根據題意,可以畫出相應的圖形,然后根據二次函數的性質和銳角三角函數可以求得點M的坐標.
解:(Ⅰ)∵點C(0,﹣3),直線y=x+m過點C和點B,
∴﹣3=0+m,得m=﹣3,
∴y=x﹣3,
當y=0時,0=x﹣3,得x=3,
∴點B的坐標為(3,0);
(Ⅱ)∵拋物線y=ax2+b過點B(3,0),點C(0,﹣3),
∴![]() ,得
,得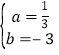 ,
,
∴拋物線的解析式為y=![]() ;
;
(Ⅲ)拋物線y=ax2+b(a≠0)上存在點M,使得∠MCB=15°,
∵點B(3,0),點C(0,﹣3),
∴OC=OB=3,
∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
當∠M1CB=15°時,設點M1的坐標為(m1,![]() ),
),
則∠M1CO=30°,
∴![]() ,
,
解得,m1=3![]() 或m1=0(舍去),
或m1=0(舍去),
當m1=3![]() 時,
時,![]() ﹣3=6,
﹣3=6,
即點M1的坐標為(3![]() ,6);
,6);
當M2CB=15°時,設點M2的坐標為(m2,![]() ),
),
則∠M2CO=60°,
∴![]() ,
,
解得,m2=![]() 或m2=0(舍去),
或m2=0(舍去),
當m2=![]() 時,
時,![]() =﹣2,
=﹣2,
即點M2的坐標為(![]() ,﹣2);
,﹣2);
由上可得,點M的坐標為(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).


科目:初中數學 來源: 題型:
【題目】(1)計算:(﹣1)2014+(sin30°)﹣1+(![]() )0﹣|3﹣
)0﹣|3﹣![]() |+83×(﹣0.125)3
|+83×(﹣0.125)3
(2)解不等式組: 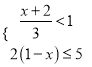 把解集在數軸上表示出來,并將解集中的整數解寫出來.
把解集在數軸上表示出來,并將解集中的整數解寫出來.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
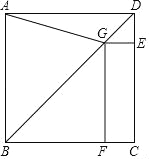
【題目】如圖,在正方形ABCD中,點G在對角線BD上(不與點B,D重合),GE⊥DC于點E,GF⊥BC于點F,連結AG.
(1)寫出線段AG,GE,GF長度之間的數量關系,并說明理由;
(2)若正方形ABCD的邊長為1,∠AGF=105°,求線段BG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
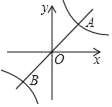
【題目】如圖,一次函數y=x的圖象與反比例函數y═![]() 的圖象交于A,B兩點,且點A坐標為(1,m).
的圖象交于A,B兩點,且點A坐標為(1,m).
(1)求此反比例函數的解析式;
(2)當x取何值時,一次函數大于反比例函數的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我縣古田鎮某紀念品商店在銷售中發現:“成功從這里開始”的紀念品平均每天可售出20件,每件盈利40元.為了擴大銷售量,增加盈利,盡快減少庫存,該商店在今年國慶黃金周期間,采取了適當的降價措施,改變營銷策略后發現:如果每件降價4元,那么平均每天就可多售出8件.商店要想平均每天在銷售這種紀念品上盈利1200元,那么每件紀念品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明坐于堤邊垂釣,如圖①,河堤AC的坡角為30°,AC長![]() 米,釣竿AO的傾斜角是60°,其長為3米,若AO與釣魚線OB的夾角為60°,求浮漂B與河堤下端C之間的距離(如圖②).
米,釣竿AO的傾斜角是60°,其長為3米,若AO與釣魚線OB的夾角為60°,求浮漂B與河堤下端C之間的距離(如圖②).
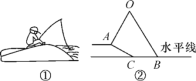
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區某校為了加強對學生的安全教育工作,開展了安全知識競賽,該校在初三年級中隨機抽取了一部分同學的競賽成績,并把抽取的競賽成績分成優、良、中、差四個等級,同時繪制了如下兩幅不完整的統計圖,請根據統計圖提供的信息解答以下問題:
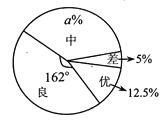
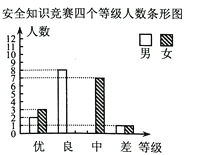
(1)該校在初三年級中隨機抽取了多少名同學的競賽成績?
(2)求扇形統計圖中![]() 的值,并補全條形統計圖;
的值,并補全條形統計圖;
(3)若從優等中選出兩名同學在全年級進行交流,請用列表或樹狀圖的方法求出所選兩名學生恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以40m/s的速度將小球沿與地面成30°角的方向擊出時,小球的飛行路線將是一條拋物線.如果不考慮空氣阻力,小球的飛行高度h(單位:m)與飛行時間t(單位:s)之間具有函數關系h=20t﹣5t2.解答以下問題
(1)小球從飛出到落地要用多少時間?
(2)小球飛行的最大高度是多少?此時需要多少飛行時間?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com