
【題目】去冬今春,某市部分地區遭受了罕見的旱災,“旱災無情人有情”.某單位給某鎮中小學捐獻一批飲用水和蔬菜共320件,其中飲用水比蔬菜多80件.
(1)、求飲用水和蔬菜各有多少件?
(2)、現計劃租用甲、乙兩種貨車共8輛,一次性將這批飲用水和蔬菜全部運往該鎮中小學.已知每輛甲種貨車最多可裝飲用水40件和蔬菜10件,每輛乙種貨車最多可裝飲用水和蔬菜各20件.則運輸部門安排甲、乙兩種貨車時有幾種方案?請你幫助設計出來;
(3)、在(2)的條件下,如果甲種貨車每輛需付運費400元,乙種貨車每輛需付運費360元.運輸部門應選擇哪種方案可使運費最少?最少運費是多少元?
【答案】(1)、飲用水和蔬菜分別為200件和120件;(2)、設計方案分別為:①甲車2輛,乙車6輛;②甲車3輛,乙車5輛;③甲車4輛,乙車4輛;(3)、甲車2輛,乙車6輛運費最少,最少運費是2960元.
【解析】
試題分析:(1)、首先設飲用水有x件,則蔬菜有(x﹣80)件,根據總件數列出方程得出答案;(2)、設租用甲種貨車m輛,則租用乙種貨車(8﹣m)輛,根據蔬菜和飲用水的件數列出不等式組,從而得出m的取值范圍,根據m為正整數,得出不同的方案;(3)、分別求出每種方案所需要的運費,然后進行比較大小,得出最小值.
試題解析:(1)、設飲用水有x件,則蔬菜有(x﹣80)件. 根據題意得:x+(x﹣80)=320,
解得x=200. ∴x﹣80=120.
答:飲用水和蔬菜分別為200件和120件;
(2)、設租用甲種貨車m輛,則租用乙種貨車(8﹣m)輛.根據題意得:![]() ,
,
解這個不等式組,得2≤m≤4. ∵m為正整數,∴m=2或3或4,安排甲、乙兩種貨車時有3種方案.
設計方案分別為:①甲車2輛,乙車6輛;②甲車3輛,乙車5輛;③甲車4輛,乙車4輛;
(3)、3種方案的運費分別為:①2×400+6×360=2960(元);②3×400+5×360=3000(元);
③4×400+4×360=3040(元);∴方案①運費最少,最少運費是2960元.
答:運輸部門應選擇甲車2輛,乙車6輛,可使運費最少,最少運費是2960元.


 名師點撥卷系列答案
名師點撥卷系列答案科目:初中數學 來源: 題型:
【題目】下列命題中,正確的有( )
①Rt△ABC中,已知兩邊長分別為3和4,則第三邊長為5;
②有一個內角等于其他兩個內角和的三角形是直角三角形;
③三角形的三邊分別為a,b,C,若a2+c2=b2,那么∠C=90°;
④若△ABC中,∠A:∠B:∠C=1:5:6,則△ABC是直角三角形.
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知下列結論:①在數軸上的點只能表示無理數;②任何一個無理數都能用數軸上的點表示;③實數與數軸上的點一一對應;④有理數有無限個,無理數有限個,其中正確的結論是( )
A.①②
B.②③
C.③④
D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,點D是AC的中點,且∠A+∠CDB=90°,過點A,D作⊙O,使圓心O在AB上,⊙O與AB交于點E.
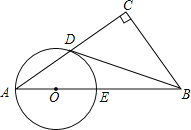
(1)求證:直線BD與⊙O相切;
(2)若AD:AE=![]() ,BC=6,求切線BD的長.
,BC=6,求切線BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=![]() x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).
x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).
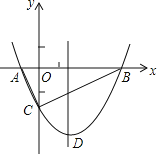
(1)求拋物線的解析式及頂點D的坐標;
(2)判斷△ABC的形狀,證明你的結論;
(3)點M是拋物線對稱軸上的一個動點,當△ACM周長最小時,求點M的坐標及△ACM的最小周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
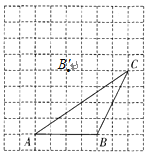
【題目】(本題8分)如下圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.
(1)△ABC的面積為 ;
(2)將△ABC經過平移后得到△A′B′C′,圖中標出了點B的對應點B',補全△A′B′C′;
(3)在圖中畫出△ABC的高CD;
(4)若連接![]() ,
, ![]() ,則這兩條線段之間的關系是 ;
,則這兩條線段之間的關系是 ;
(5)能使S△ABC=S△QBC的格點Q,共有 個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com