
【題目】已知函數f(x)=Acos2(x+φ)+1(A>0,>0,0<φ< ![]() )的最大值為3,f(x)的圖象與y軸的交點坐標為(0,2),其相鄰兩條對稱軸間的距離為2,則f(1)+f(2)+f(3)+…+f(2016)的值為( )
)的最大值為3,f(x)的圖象與y軸的交點坐標為(0,2),其相鄰兩條對稱軸間的距離為2,則f(1)+f(2)+f(3)+…+f(2016)的值為( )
A.2468
B.3501
C.4032
D.5739
【答案】C
【解析】解:∵函數f(x)=Acos2(ωx+φ)+1=A ![]() +1 =
+1 = ![]() cos(2ωx+2φ)+1+
cos(2ωx+2φ)+1+ ![]() (A>0,ω>0,0<φ<
(A>0,ω>0,0<φ< ![]() )的最大值為3,
)的最大值為3,
∴ ![]() +1+
+1+ ![]() =3,可求:A=2.
=3,可求:A=2.
∵函數圖象相鄰兩條對稱軸間的距離為2,可得函數的最小正周期為4,即: ![]() =4,
=4,
∴解得:ω= ![]() .
.
又∵f(x)的圖象與y軸的交點坐標為(0,2),可得:cos(2φ)+1+1=2,
∴cos2φ=0,2φ= ![]() ,解得:φ=
,解得:φ= ![]() .
.
∴函數的解析式為:f(x)=cos( ![]() x+
x+ ![]() )+2=﹣sin
)+2=﹣sin ![]() x+2,
x+2,
∴f(1)+f(2)+…+f(2016)=﹣(sin ![]() +sin
+sin ![]() +sin
+sin ![]() +…+sin
+…+sin ![]() )+2×2016
)+2×2016
=504×0+4032=4032.
故選:C.
由條件利用二倍角的余弦公式可得f(x)= ![]() cos(2ωx+2φ)+1+
cos(2ωx+2φ)+1+ ![]() ,由函數的最值求出A,由周期求出ω,由特殊點的坐標求出φ的值,可得函數的解析式,再利用函數的周期性求得所求式子的值.
,由函數的最值求出A,由周期求出ω,由特殊點的坐標求出φ的值,可得函數的解析式,再利用函數的周期性求得所求式子的值.


科目:初中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集為{x|﹣2≤x≤3},求實數a的值;
(2)在(1)的條件下,若存在實數n使f(n)≤m﹣f(﹣n)成立,求實數m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ![]() ,求函數f(x)的單調區間;
,求函數f(x)的單調區間;
(2)當x≥0時,不等式f(x)≤ex恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,設橢圓C1: ![]() +
+ ![]() =1(a>b>0),長軸的右端點與拋物線C2:y2=8x的焦點F重合,且橢圓C1的離心率是
=1(a>b>0),長軸的右端點與拋物線C2:y2=8x的焦點F重合,且橢圓C1的離心率是 ![]() .
. 
(1)求橢圓C1的標準方程;
(2)過F作直線l交拋物線C2于A,B兩點,過F且與直線l垂直的直線交橢圓C1于另一點C,求△ABC面積的最小值,以及取到最小值時直線l的方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市儲運部緊急調撥一批物資,調進物資共用4h,調進物資2h后開始調出物資(調進物資與調出物資的速度探持不變).儲運部庫存物資![]() (t)與時間
(t)與時間![]() (h)之間的函數關系如圖所示,這批物資從開始調進到全部調出需要的時間是( )
(h)之間的函數關系如圖所示,這批物資從開始調進到全部調出需要的時間是( )

A. 4 h B. 4.4 h C. 4.8 h D. 5 h
查看答案和解析>>
科目:初中數學 來源: 題型:
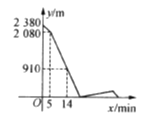
【題目】![]() 兩地之間的路程為2 380 m,甲、乙兩人分別從
兩地之間的路程為2 380 m,甲、乙兩人分別從![]() 兩地出發,相向而行.已知甲先出發5 min后,乙才出發,他們兩人在
兩地出發,相向而行.已知甲先出發5 min后,乙才出發,他們兩人在![]() 之間的
之間的![]() 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回![]() 地,乙繼續向
地,乙繼續向![]() 地前行.甲到達
地前行.甲到達![]() 地時停止行走,乙到達
地時停止行走,乙到達![]() 地時也停止行走,在整個行走過程中,甲、乙兩人均保持各自的速度勻速行走,甲、乙兩人相距的路程
地時也停止行走,在整個行走過程中,甲、乙兩人均保持各自的速度勻速行走,甲、乙兩人相距的路程![]() (m)與甲出發的時間
(m)與甲出發的時間![]() (min)之間的關系如圖所示,則乙到達
(min)之間的關系如圖所示,則乙到達![]() 地時,甲與
地時,甲與![]() 地相距的路程是
地相距的路程是
________m.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直角坐標系中有一矩形OABC , 其中 O是坐標原點,點A , C分別在x軸和y軸上,點B的坐標為(3,4),直線 ![]() 交AB于點D , 點P是直線
交AB于點D , 點P是直線 ![]() 位于第一象限上的一點,連接PA , 以PA為半徑作⊙P ,
位于第一象限上的一點,連接PA , 以PA為半徑作⊙P , 
(1)連接AC , 當點P落在AC上時, 求PA的長;
(2)當⊙P經過點O時,求證:△PAD是等腰三角形;
(3)設點P的橫坐標為m ,
在點P移動的過程中,當⊙P與矩形OABC某一邊的交點恰為該邊的中點時,求所有滿足要求的m值;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實數tan45°,![]() ,0,﹣
,0,﹣![]() π,
π,![]() ,﹣
,﹣![]() ,sin60°,0.3131131113…(相鄰兩個3之間依次多一個1),其中無理數的個數是( )
,sin60°,0.3131131113…(相鄰兩個3之間依次多一個1),其中無理數的個數是( )
A.4
B.2
C.1
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com