
【題目】如圖,拋物線經過點A(1,0),B(5,0),C(0,![]() )三點,頂點為D,設點E(x,y)是拋物線上一動點,且在x軸下方.
)三點,頂點為D,設點E(x,y)是拋物線上一動點,且在x軸下方.
(1)求拋物線的解析式;
(2)當點E(x,y)運動時,試求三角形OEB的面積S與x之間的函數關系式,并求出面積S的最大值?
(3)在y軸上確定一點M,使點M到D、B兩點距離之和d=MD+MB最小,求點M的坐標.

【答案】(1)y=![]() x2﹣4x+
x2﹣4x+![]() ;(2)S=﹣
;(2)S=﹣![]() (x﹣3)2+
(x﹣3)2+![]() (1<x<5),當x=3時,S有最大值
(1<x<5),當x=3時,S有最大值![]() ;(3)(0,﹣
;(3)(0,﹣![]() )
)
【解析】
(1)設出解析式,由待定系數法可得出結論;
(2)點E在拋物線上,用x去表示y,結合三角形面積公式即可得出三角形OEB的面積S與x之間的函數關系式,再由E點在x軸下方,得出1<x<5,將三角形OEB的面積S與x之間的函數關系式配方,即可得出最值;
(3)找出D點關于y軸對稱的對稱點D′,結合三角形內兩邊之和大于第三邊,即可確定當MD+MB最小時M點的坐標.
解:(1)設拋物線解析式為y=ax2+bx+c,則
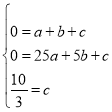 ,解得:
,解得: .
.
故拋物線解析式為y=![]() x2﹣4x+
x2﹣4x+![]() .
.
(2)過點E作EF⊥x軸,垂足為點F,如圖1所示.

E點坐標為(x,![]() x2﹣4x+
x2﹣4x+![]() ),F點的坐標為(x,0),
),F點的坐標為(x,0),
∴EF=0﹣(![]() x2﹣4x+
x2﹣4x+![]() )=﹣
)=﹣![]() x2+4x﹣
x2+4x﹣![]() .
.
∵點E(x,y)是拋物線上一動點,且在x軸下方,
∴1<x<5.
三角形OEB的面積S=![]() OBEF=
OBEF=![]() ×5×(﹣
×5×(﹣![]() x2+4x﹣
x2+4x﹣![]() )=﹣
)=﹣![]() (x﹣3)2+
(x﹣3)2+![]() (1<x<5=.
(1<x<5=.
當x=3時,S有最大值![]() .
.
(3)作點D關于y軸的對稱點D′,連接BD′,如圖2所示.

∵拋物線解析式為y=![]() x2﹣4x+
x2﹣4x+![]() =
=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴D點的坐標為(3,﹣![]() ),
),
∴D′點的坐標為(﹣3,﹣![]() ).
).
由對稱的特性可知,MD=MD′,
∴MB+MD=MB+MD′,
當B、M、D′三點共線時,MB+MD′最小.
設直線BD′的解析式為y=kx+b,則
 ,解得:
,解得: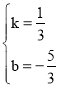 ,
,
∴直線BD′的解析式為y=![]() x﹣
x﹣![]() .
.
當x=0時,y=﹣![]() ,
,
∴點M的坐標為(0,﹣![]() ).
).


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
【題目】(閱讀材料)某校九年級數學課外興趣探究小組在學習完《第二十八章銳角三角函數》后,利用所學知識進行深度探究,得到以下正確的等量關系式:
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
(理解應用)請你利用以上信息求下列各式的值:(1)![]() ;(2)
;(2)![]()
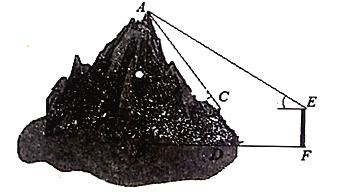
(拓展應用)(3)為了求出海島上的山峰![]() 的高度,在
的高度,在![]() 處和
處和![]() 處樹立標桿
處樹立標桿![]() 和
和![]() ,標桿的高都是3丈,
,標桿的高都是3丈,![]() 兩處相隔1000步(1步等于6尺),并且
兩處相隔1000步(1步等于6尺),并且![]() 和
和![]() 在同一平面內,在標桿
在同一平面內,在標桿![]() 的頂端
的頂端![]() 處測得山峰頂端
處測得山峰頂端![]() 的仰角75°,在標桿
的仰角75°,在標桿![]() 的頂端
的頂端![]() 處測得山峰頂端
處測得山峰頂端![]() 的仰角30°,山峰的高度即
的仰角30°,山峰的高度即![]() 的長是多少步?(結果保留整數)(參考數據:
的長是多少步?(結果保留整數)(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按如下方法,將△ABC的三邊縮小到原來的![]() ,如圖,任取一點O,連結AO,BO,CO,并取它們的中點D、E、F,得△DEF;則下列說法錯誤的是( )
,如圖,任取一點O,連結AO,BO,CO,并取它們的中點D、E、F,得△DEF;則下列說法錯誤的是( )
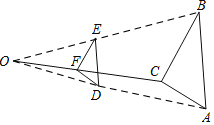
A.點O為位似中心且位似比為1:2
B.△ABC與△DEF是位似圖形
C.△ABC與△DEF是相似圖形
D.△ABC與△DEF的面積之比為4:1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,己知點![]() ,點
,點![]() 在
在![]() 軸上,并且
軸上,并且![]() ,動點
,動點![]() 在過
在過![]() 三點的拋物線上.
三點的拋物線上.
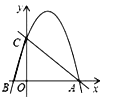
(1)求拋物線的解析式.
(2)作垂直![]() 軸的直線,在第一象限交直線
軸的直線,在第一象限交直線![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() ,求當線段
,求當線段![]() 的長有最大值時
的長有最大值時![]() 的坐標.并求出
的坐標.并求出![]() 最大值是多少.
最大值是多少.
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使得△
,使得△![]() 是等腰三角形?若存在,請直接寫出點
是等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
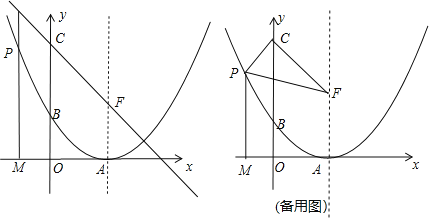
【題目】如圖,已知點C(0,3),拋物線的頂點為A(2,0),與y軸交于點B(0,1),F在拋物線的對稱軸上,且縱坐標為1.點P是拋物線上的一個動點,過點P作PM⊥x軸于點M,交直線CF于點H,設點P的橫坐標為m.
(1)求拋物線的解析式;
(2)若點P在直線CF下方的拋物線上,用含m的代數式表示線段PH的長,并求出線段PH的最大值及此時點P的坐標;
(3)當PF﹣PM=1時,若將“使△PCF面積為2”的點P記作“巧點”,則存在多個“巧點”,且使△PCF的周長最小的點P也是一個“巧點”,請直接寫出所有“巧點”的個數,并求出△PCF的周長最小時“巧點”的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
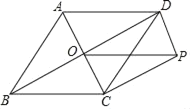
【題目】如圖,在菱形ABCD中,AC、BD交于點O,BD=8,AC=4,DP∥AC,CP∥BD.
(1)求線段OP的長;
(2)不添加任何輔助線的情況下,直接寫出圖中所有的平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學計劃根據學生的興趣愛好組建課外興趣小組,并隨機抽取了部分同學的興趣愛好進行調查,將收集的數據整理并繪制成下列兩幅統計圖,請根據圖中的信息,完成下列問題:

![]() 學校這次調查共抽取了 名學生;
學校這次調查共抽取了 名學生;
![]() 求
求![]() 的值并補全條形統計圖;
的值并補全條形統計圖;
![]() 在扇形統計圖中,“圍棋”所在扇形的圓心角度數為 ;
在扇形統計圖中,“圍棋”所在扇形的圓心角度數為 ;
![]() 設該校共有學生
設該校共有學生![]() 名,請你估計該校有多少名學生喜歡足球.
名,請你估計該校有多少名學生喜歡足球.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.
,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.

(1)求證:△AEF≌△DEB;
(2)證明四邊形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】京沈高速鐵路赤峰至喀左段正在建設中,甲、乙兩個工程隊計劃參與一項工程建設,甲隊單獨施工30天完成該項工程的![]() ,這時乙隊加入,兩隊還需同時施工15天,才能完成該項工程.
,這時乙隊加入,兩隊還需同時施工15天,才能完成該項工程.
(1)若乙隊單獨施工,需要多少天才能完成該項工程?
(2)若甲隊參與該項工程施工的時間不超過36天,則乙隊至少施工多少天才能完成該項工程?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com