
【題目】把下列各數分別填入相應的集合中:-(-230),![]() ,0,-0.99,1.31,5,
,0,-0.99,1.31,5,![]() ,3.14246792…,-
,3.14246792…,-![]() .
.
(1)整數集合:{ …}
(2)非正數集合:{ …}
(3)正有理數集合:{ …}
(4)無理數集合:{ …}
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,已知直線![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,射線
,射線![]() 從
從![]() 位置起始,繞點
位置起始,繞點![]() 逆時針旋轉,終邊
逆時針旋轉,終邊![]() 與始邊
與始邊![]() 形成的角度為
形成的角度為![]() .
.
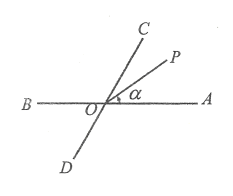
問題1:若![]() 逆時針旋轉
逆時針旋轉![]() 停止,則
停止,則
(1)![]() __________________時,
__________________時,![]() 平分
平分![]() ;
;
(2)![]() __________________時,
__________________時,![]() ;
;
(3)![]() __________________時,
__________________時,![]() ;
;
問題2:若![]() 逆時針旋轉的速度為每秒
逆時針旋轉的速度為每秒![]() ,在
,在![]() 勻速旋轉的同時,直線
勻速旋轉的同時,直線![]() 也從圖的位置開始繞點
也從圖的位置開始繞點![]() 逆時針勻速旋轉,旋轉速度為每秒
逆時針勻速旋轉,旋轉速度為每秒![]() ,當
,當![]() 完成旋轉一周時,
完成旋轉一周時,![]() 也同時停止旋轉.設旋轉時間為
也同時停止旋轉.設旋轉時間為![]() (
(![]() )秒.
)秒.
(1)旋轉時間![]() 為多少時,射線
為多少時,射線![]() 與
與![]() 重合.請寫出求解過程.
重合.請寫出求解過程.
(2)觀察旋轉全過程,判斷旋轉時間![]() 為多少時,射線
為多少時,射線![]() 平分
平分![]() .請直接寫出
.請直接寫出![]() 的值.(注:
的值.(注:![]() 指大于
指大于![]() 且小于
且小于![]() 的角)
的角)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線EF,CD相交于點0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度數;
(2)若∠AOE=α,求∠BOD的度數;(用含α的代數式表示)
(3)從(1)(2)的結果中能看出∠AOE和∠BOD有何關系?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司有10名銷售業務員,去年每人完成的銷售額情況如表:

(1)求10名銷售員銷售額的平均數、中位數和眾數.(單位:萬元)
(2)為了調動員工積極性,公司準備采取超額有獎措施,請問把標準定為多少萬元時最合適?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生參加社團的情況,從2010年起,某市教育部門每年都從全市所有學生中隨機抽取2000名學生進行調查,圖①、圖②是部分調查數據的統計圖(參加社團的學生每人只能報一項)根據統計圖提供的信息解決下列

問題:
(1)求圖②中“科技類”所在扇形的圓心角α的度數
(2)該市2012年抽取的學生中,參加體育類與理財類社團的學生共有多少人?
(3)該市2014年共有50000名學生,請你估計該市2014年參加社團的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是將拋物線 ![]() 平移后得到的拋物線,其對稱軸為
平移后得到的拋物線,其對稱軸為 ![]() ,與x軸的一個交點為A
,與x軸的一個交點為A ![]() ,另一交點為B,與y軸交點為C.
,另一交點為B,與y軸交點為C.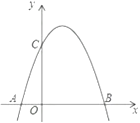
(1)求拋物線的函數表達式;
(2)若點 ![]() 為拋物線上一點,且BC⊥NC,求點N的坐標;
為拋物線上一點,且BC⊥NC,求點N的坐標;
(3)點P是拋物線上一點,點Q是一次函數 ![]() 的圖象上一點,若四邊形OAPQ為平行四邊形,這樣的點P、Q是否存在?若存在,分別求出點P、Q的坐標,若不存在,說明理由.
的圖象上一點,若四邊形OAPQ為平行四邊形,這樣的點P、Q是否存在?若存在,分別求出點P、Q的坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,反比例函數y= ![]() (x>0)的圖象和矩形ABCD在第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標為(2,6).
(x>0)的圖象和矩形ABCD在第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標為(2,6).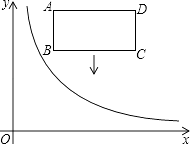
(1)直接寫出B、C、D三點的坐標;
(2)若將矩形向下平移,矩形的兩個頂點恰好同時落在反比例函數的圖象上,猜想這是哪兩個點,并求矩形的平移距離和反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,△ABC與△DEC關于點C成中心對稱,連接AE、BD.
(1)線段AE、BD具有怎樣的位置關系和大小關系?說明你的理由.
(2)如果△ABC的面積為5cm2 , 求四邊形ABDE的面積.
(3)當∠ACB為多少度時,四邊形ABDE為矩形?說明你的理由.
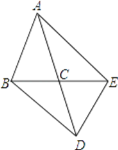
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:如圖(1),點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,試判斷BE、EF、FD之間的數量關系.
【發現證明】小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖(1)證明上述結論.
【類比引申】如圖(2),四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時,仍有EF=BE+FD;請證明你的結論.
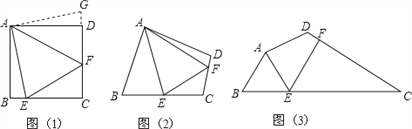
【探究應用】如圖(3),在某公園的同一水平面上,四條通道圍成四邊形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分別有景點E、F,且AE⊥AD,DF=40(![]() ﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據:
﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com