解:過D作DE⊥AB于E,分為三種情況:
①如圖1,當P在AD上時,此時0≤x≤6,

∵D(6,3),
∴OE=6,DE=3,
∵MN⊥AB.DE⊥AB,
∴PQ∥DE,
∴△AQP∽△AED,
∴
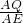
=

,
∴

=
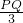
,
PQ=

x,
∴S=S
△APQ=

×AQ×PQ=

•x•

x=

x
2;
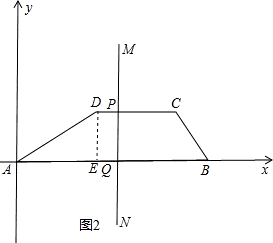
②如圖2,P在DC上,此時6<x≤12,
DP=EQ=x-6,PQ=DE=3,AQ=x,
S=S
四邊形ADPQ=

×(DP+AQ)×PQ=

•(x-6+x)•3=3x-9;
③如圖3,P在BC上,此時12<x<15,
過C作CF⊥AB于F
則PQ∥CF,
∵B(15,0),C(12.3),D(6,3),
∴CF=3,BA=15,BQ=15-x,BF=15-12,DC=12-6=6,
∵CF∥PQ,

∴△PQB∽△CFB,
∴

=
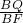
,
∴
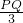
=

,
PQ=15-x,
∴S=S
五邊形ADCPQ=S
梯形ABCD-S
△BPQ=

×(DC+AB)×CF-

×BQ×PQ
=

×(6+15)×3-

•(15-x)•(15-x)
=-

x
2+15x-81,
④當x≥15時,S=S
梯形ABCD=

×(6+15)×3=31.5;
綜合上述,S=

.
分析:過D作DE⊥AB于E,畫出符合的四種情況,根據A、B、C、D的坐標求出PQ的值,根據面積公式求出即可.
點評:本題考查了相似三角形的性質和判定和分段函數,關鍵是求出符合條件的所有情況,用了分類討論思想.

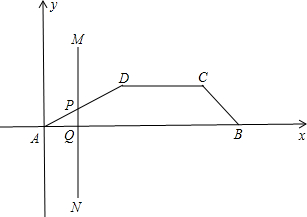 如圖,在計算機屏幕上有一梯形ABCD,AB∥CD,A在坐標原點,B(15,0),C(12.3),D(6,3),MN是垂直于x軸的一條直線,MN與梯形的邊交于P,Q兩點.當MN從y軸向右移動時.梯形中被MN掃過的部分將改變顏色.設AQ=x,顏色改變部分的面積為S,求以x為自變量S的函數關系式.
如圖,在計算機屏幕上有一梯形ABCD,AB∥CD,A在坐標原點,B(15,0),C(12.3),D(6,3),MN是垂直于x軸的一條直線,MN與梯形的邊交于P,Q兩點.當MN從y軸向右移動時.梯形中被MN掃過的部分將改變顏色.設AQ=x,顏色改變部分的面積為S,求以x為自變量S的函數關系式.
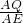 =
= ,
, =
=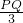 ,
, x,
x, ×AQ×PQ=
×AQ×PQ= •x•
•x• x=
x= x2;
x2; ②如圖2,P在DC上,此時6<x≤12,
②如圖2,P在DC上,此時6<x≤12, ×(DP+AQ)×PQ=
×(DP+AQ)×PQ= •(x-6+x)•3=3x-9;
•(x-6+x)•3=3x-9; ∴△PQB∽△CFB,
∴△PQB∽△CFB, =
=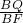 ,
,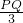 =
= ,
, ×(DC+AB)×CF-
×(DC+AB)×CF- ×BQ×PQ
×BQ×PQ ×(6+15)×3-
×(6+15)×3- •(15-x)•(15-x)
•(15-x)•(15-x) x2+15x-81,
x2+15x-81, ×(6+15)×3=31.5;
×(6+15)×3=31.5; .
.

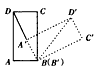
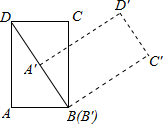 如圖,在計算機白色屏幕上有一個矩形畫刷ABCD,它的邊AB=1,AD=
如圖,在計算機白色屏幕上有一個矩形畫刷ABCD,它的邊AB=1,AD= 如圖,在計算機的白色屏幕上有一個矩形刷ABCD,AB=1,AD=
如圖,在計算機的白色屏幕上有一個矩形刷ABCD,AB=1,AD= 如圖,在計算機屏幕上有一梯形ABCD,AB∥CD,A在坐標原點,B(15,0),C(12.3),D(6,3),MN是垂直于x軸的一條直線,MN與梯形的邊交于P,Q兩點.當MN從y軸向右移動時.梯形中被MN掃過的部分將改變顏色.設AQ=x,顏色改變部分的面積為S,求以x為自變量S的函數關系式.
如圖,在計算機屏幕上有一梯形ABCD,AB∥CD,A在坐標原點,B(15,0),C(12.3),D(6,3),MN是垂直于x軸的一條直線,MN與梯形的邊交于P,Q兩點.當MN從y軸向右移動時.梯形中被MN掃過的部分將改變顏色.設AQ=x,顏色改變部分的面積為S,求以x為自變量S的函數關系式. ,把ABCD以點B為中心按順時針方向旋轉60°,則被這個畫刷著色的面積為( )(注意:所謂畫刷,就是屏幕上的一個矩形塊,它在屏幕上移動或轉動時,掃過的部分將改變顏色)。
,把ABCD以點B為中心按順時針方向旋轉60°,則被這個畫刷著色的面積為( )(注意:所謂畫刷,就是屏幕上的一個矩形塊,它在屏幕上移動或轉動時,掃過的部分將改變顏色)。