
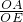 =
= ,
, ,
, -1;
-1;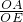 =
=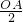 ,
, =
=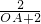 ,
,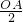 =
=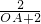 ,
, ,
, -1;
-1; ,
, -1;
-1; ×22=
×22=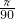 n(cm2),
n(cm2),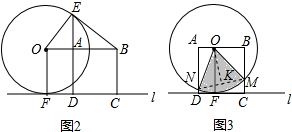
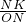 =
=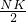 ,
, π(cm2),
π(cm2), π≤S扇形MON≤π.
π≤S扇形MON≤π.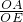 =
= ,進而求出OA即可;
,進而求出OA即可; ×22=
×22=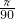 n進而利用函數增減性分析①當N,M,A分別與D,B,O重合時,MN最大,②當MN=DC=2時,MN最小,分別求出即可.
n進而利用函數增減性分析①當N,M,A分別與D,B,O重合時,MN最大,②當MN=DC=2時,MN最小,分別求出即可.

 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(湖北宜昌卷)數學(解析版) 題型:解答題
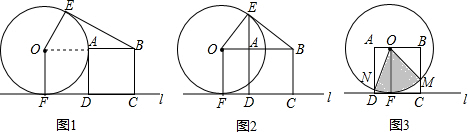
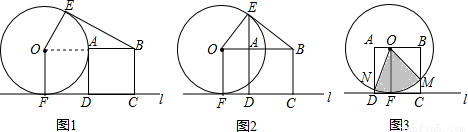
半徑為2cm的與⊙O邊長為2cm的正方形ABCD在水平直線l的同側,⊙O與l相切于點F,DC在l上.
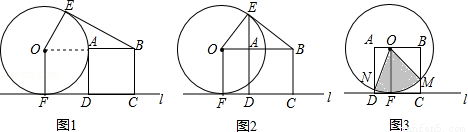
(1)過點B作的一條切線BE,E為切點.
①填空:如圖1,當點A在⊙O上時,∠EBA的度數是 ;
②如圖2,當E,A,D三點在同一直線上時,求線段OA的長;
(2)以正方形ABCD的邊AD與OF重合的位置為初始位置,向左移動正方形(圖3),至邊BC與OF重合時結束移動,M,N分別是邊BC,AD與⊙O的公共點,求扇形MON的面積的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
半徑為2cm的與⊙O邊長為2cm的正方形ABCD在水平直線l的同側,⊙O與l相切于點F,DC在l上.
(1)過點B作的一條切線BE,E為切點.
①填空:如圖1,當點A在⊙O上時,∠EBA的度數是 30° ;
②如圖2,當E,A,D三點在同一直線上時,求線段OA的長;
(2)以正方形ABCD的邊AD與OF重合的位置為初始位置,向左移動正方形(圖3),至邊BC與OF重合時結束移動,M,N分別是邊BC,AD與⊙O的公共點,求扇形MON的面積的范圍.
查看答案和解析>>
科目:初中數學 來源:2013年湖北省宜昌市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com