
【題目】如圖①,在Rt△ABC中,∠C=90°,AB=10,BC=6,點P從點A出發,沿折線AB﹣BC向終點C運動,在AB上以每秒5個單位長度的速度運動,在BC上以每秒3個單位長度的速度運動,點Q從點C出發,沿CA方向以每秒![]() 個單位長度的速度運動,P,Q兩點同時出發,當點P停止時,點Q也隨之停止.設點P運動的時間為t秒.
個單位長度的速度運動,P,Q兩點同時出發,當點P停止時,點Q也隨之停止.設點P運動的時間為t秒.
(1)求線段AQ的長;(用含t的代數式表示)
(2)連結PQ,當PQ與△ABC的一邊平行時,求t的值;
(3)如圖②,過點P作PE⊥AC于點E,以PE,EQ為鄰邊作矩形PEQF,點D為AC的中點,連結DF.設矩形PEQF與△ABC重疊部分圖形的面積為S.
①當點Q在線段CD上運動時,求S與t之間的函數關系式;
②直接寫出DF將矩形PEQF分成兩部分的面積比為1:2時t的值.

【答案】(1)AQ=8﹣![]() t(0≤t≤4);(2)t=
t(0≤t≤4);(2)t=![]() s或3s;(3)①
s或3s;(3)①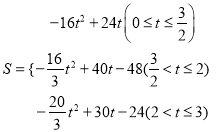 ;②t=
;②t=![]() s或
s或![]() s.
s.
【解析】試題分析:(1)利用勾股定理先求出AC,根據AQ=AC﹣CQ即可解決問題;
(2)分兩種情形列出方程求解即可;
(3)①分三種情形a、如圖1中,當0≤t≤![]() 時,重疊部分是四邊形PEQF.b、如圖2中,當
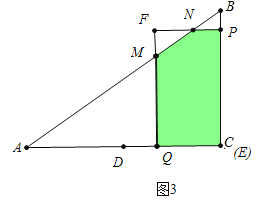
時,重疊部分是四邊形PEQF.b、如圖2中,當![]() <t≤2時,重疊部分是四邊形PNQE.C、如圖3中,當2<t≤3時,重疊部分是五邊形MNPBQ.分別求解即可;
<t≤2時,重疊部分是四邊形PNQE.C、如圖3中,當2<t≤3時,重疊部分是五邊形MNPBQ.分別求解即可;
②分兩種情形a、如圖4中,當DE:DQ=1:2時,DF將矩形PEQF分成兩部分的面積比為1:2.b、如圖5中,當NE:PN=1:2時,DF將矩形PEQF分成兩部分的面積比為1:2.分別列出方程即可解決問題;
試題解析:解:(1)在Rt△ABC中,∵∠C=90°,AB=10,BC=6,∴AC=![]() =
=![]() =8,∵CQ=
=8,∵CQ=![]() t,∴AQ=8﹣
t,∴AQ=8﹣![]() t(0≤t≤4).
t(0≤t≤4).
(2)①當PQ∥BC時, ![]() ,∴
,∴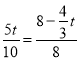 ,∴t=
,∴t=![]() s.
s.
②當PQ∥AB時, ![]() ,∴
,∴ ,∴t=3.
,∴t=3.
綜上所述,t=![]() s或3s時,當PQ與△ABC的一邊平行.
s或3s時,當PQ與△ABC的一邊平行.
(3)①如圖1中,a、當0≤t≤![]() 時,重疊部分是四邊形PEQF.
時,重疊部分是四邊形PEQF.
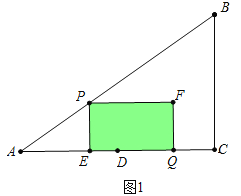
S=PEEQ=3t(8﹣4t﹣![]() t)=
t)=![]() .
.
b、如圖2中,當![]() <t≤2時,重疊部分是四邊形PNQE.
<t≤2時,重疊部分是四邊形PNQE.
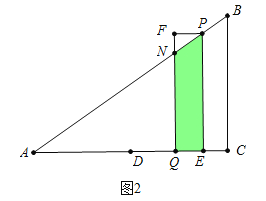
S=S四邊形PEQF﹣S△PFN=(16t2﹣24t)﹣![]()
![]() [5t﹣
[5t﹣![]() (8﹣
(8﹣![]() t)]
t)] ![]() [5t﹣
[5t﹣![]() (8﹣
(8﹣![]() t0]=
t0]= ![]() .
.
C.如圖3中,當2<t≤3時,重疊部分是五邊形MNPBQ.
S =S四邊形PBQF -S△FNM=![]() t[6﹣3(t﹣2)]﹣
t[6﹣3(t﹣2)]﹣![]() [
[![]() t﹣4(t﹣2)]
t﹣4(t﹣2)] ![]() [
[![]() t﹣4(t﹣2)]=
t﹣4(t﹣2)]= ![]() .
.
綜上所述: 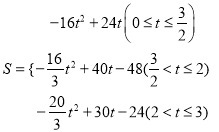 ;
;
②a、如圖4中,當DE:DQ=1:2時,DF將矩形PEQF分成兩部分的面積比為1:2.
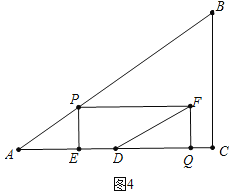
則有(4﹣4t):(4﹣![]() t)=1:2,解得t=
t)=1:2,解得t=![]() s;
s;
b、如圖5中,當NE:PN=1:2時,DF將矩形PEQF分成兩部分的面積比為1:2.
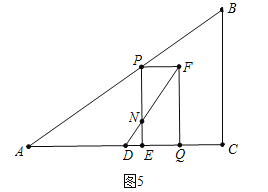
∴DE:DQ=NE:FQ=1:3,∴(4t﹣4):(4﹣![]() t)=1:3,解得t=
t)=1:3,解得t=![]() s.
s.
綜上所述,當t=![]() s或
s或![]() s時,DF將矩形PEQF分成兩部分的面積比為1:2.
s時,DF將矩形PEQF分成兩部分的面積比為1:2.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC, 點M在△ABC內,點P在線段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若點M在底邊BC的中線上,且BP=AC,試探究∠A與∠ABP之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分別是BC,DE的中點.
(1)求證:MN⊥DE;
(2)若BC=20,DE=12,求△MDE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于給定的兩個函數,任取自變量x的一個值,當x<0時,它們對應的函數值互為相反數;當x≥0時,它們對應的函數值相等,我們稱這樣的兩個函數互為相關函數.例如:一次函數y=x﹣1,它的相關函數為 .
.
(1)已知點A(﹣5,8)在一次函數y=ax﹣3的相關函數的圖象上,求a的值;
(2)已知二次函數![]() .
.
①當點B(m, ![]() )在這個函數的相關函數的圖象上時,求m的值;
)在這個函數的相關函數的圖象上時,求m的值;
②當﹣3≤x≤3時,求函數![]() 的相關函數的最大值和最小值;
的相關函數的最大值和最小值;
(3)在平面直角坐標系中,點M,N的坐標分別為(﹣![]() ,1),(
,1),(![]() ,1}),連結MN.直接寫出線段MN與二次函數
,1}),連結MN.直接寫出線段MN與二次函數![]() 的相關函數的圖象有兩個公共點時n的取值范圍.
的相關函數的圖象有兩個公共點時n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過點A(2,0)的兩條直線l1,l2分別交y軸于點B,C,其中點B在原點上方,點C在原點下方,已知AB=![]() .
.
(1)求點B的坐標;
(2)若△ABC的面積為4,求直線l2的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)請判斷AB與CD的位置關系并說明理由;
(2)如圖2,在(1)的結論下,當∠E=90°保持不變,移動直角頂點E,使∠MCE=∠ECD,當直角頂點E點移動時,問∠BAE與∠MCD是否存在確定的數量關系?

(3)如圖3,在(1)的結論下,P為線段AC上一定點,點Q為直線CD上一動點,當點Q在射線CD上運動時(點C除外)∠CPQ+∠CQP與∠BAC有何數量關系? (2、3小題只需選一題說明理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩商場自行定價銷售某一商品.
(1)甲商場將該商品提價15%后的售價為1.15元,則該商品在甲商場的原價為 ▲ 元;
(2)乙商場將該商品提價20%后,用6元錢購買該商品的件數比沒提價前少買1件,求該商品在乙商場的原價是多少?
(3)在(1)、(2)小題的條件下,甲、乙兩商場把該商品均按原價進行了兩次價格調整.
甲商場:第一次提價的百分率是![]() ,第二次提價的百分率是
,第二次提價的百分率是![]() ;
;
乙商場:兩次提價的百分率都是![]() (
(![]() .
.
請問甲、乙兩商場,哪個商場的提價較多?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CA=CB,∠ACB=90°,以AB的中點D為圓心,作圓心角為90°的扇形DEF,點C恰在EF上,設∠BDF=α(0°<α<90°),當α由小到大變化時,圖中陰影部分的面積( )

A. 由小到大 B. 由大到小 C. 不變 D. 先由小到大,后由大到小
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com