
【題目】某食品廠生產一種半成品食材,成本為2元/千克,每天的產量![]() (百千克)與銷售價格
(百千克)與銷售價格![]() (元/千克)滿足函數關系式
(元/千克)滿足函數關系式![]() ,從市場反饋的信息發現,該半成品食材每天的市場需求量
,從市場反饋的信息發現,該半成品食材每天的市場需求量![]() (百千克)與銷售價格
(百千克)與銷售價格![]() (元/千克)滿足一次函數關系,部分數據如表:
(元/千克)滿足一次函數關系,部分數據如表:
銷售價格 | 2 | 4 | …… | 10 |
市場需求量 | 12 | 10 | …… | 4 |
已知按物價部門規定銷售價格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接寫出![]() 與
與![]() 的函數關系式,并注明自變量
的函數關系式,并注明自變量![]() 的取值范圍;
的取值范圍;
(2)當每天的產量小于或等于市場需求量時,這種半成品食材能全部售出,而當每天的產量大于市場需求量時,只能售出符合市場需求量的半成品食材,剩余的食材由于保質期短而只能廢棄.
①當每天的半成品食材能全部售出時,求![]() 的取值范圍;
的取值范圍;
②求廠家每天獲得的利潤y(百元)與銷售價格![]() 的函數關系式;
的函數關系式;
(3)在(2)的條件下,當![]() 為______元/千克時,利潤
為______元/千克時,利潤![]() 有最大值;若要使每天的利潤不低于24(百元),并盡可能地減少半成品食材的浪費,則
有最大值;若要使每天的利潤不低于24(百元),并盡可能地減少半成品食材的浪費,則![]() 應定為______元/千克.
應定為______元/千克.
【答案】(1)![]() ,其中
,其中![]() ;(2)
;(2)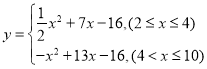 ;(3)
;(3)![]() ,5
,5
【解析】
(1)設![]() 與
與![]() 的函數關系式為:
的函數關系式為:![]() ,根據表格中的數據利用待定系數法進行求解即可;
,根據表格中的數據利用待定系數法進行求解即可;
(2)①當每天的半成品食材能全部售出時,有![]() ,據此列不等式進行求解即可;
,據此列不等式進行求解即可;
②根據自變量為![]() 、
、![]() 兩種情況分別列式進行求解即可;
兩種情況分別列式進行求解即可;
(3)根據(2)中的情況利用二次函數的性質分別進行討論即可求得答案.
(1)由表格的數據,設![]() 與
與![]() 的函數關系式為:
的函數關系式為:![]() ,
,
根據表格的數據得![]() ,解得
,解得![]() ,
,
故![]() 與
與![]() 的函數關系式為:
的函數關系式為:![]() ,其中
,其中![]() ;
;
(2)①當每天的半成品食材能全部售出時,有![]() ,
,
即![]() ,解得
,解得![]() ,
,
又![]() ,所以此時
,所以此時![]() ,
,
②由①可知,當![]() 時,
時,
![]() ,
,
當![]() 時,
時,![]()
![]()
![]() ,
,
即有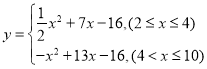 ;
;
(3)當![]() 時,
時,
![]() 的對稱軸為
的對稱軸為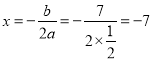 ,
,
∴當![]() 時,y隨著x的增大而增大,
時,y隨著x的增大而增大,
∴![]() 時有最大值,
時有最大值,![]() ,
,
當![]() 時,
時,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 時取最大值,
時取最大值,
即此時![]() 有最大利潤,
有最大利潤,
要使每天的利潤不低于24百元,則當![]() 時,顯然不符合,
時,顯然不符合,
故![]() ,解得
,解得![]() ,
,
故當![]() 時,能保證不低于24百元,
時,能保證不低于24百元,
故答案為:![]() ,5.
,5.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A是拋物線![]() 對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為______________.
對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
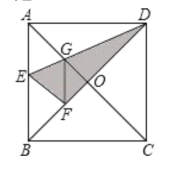
【題目】如圖,在正方形紙片![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() ,折疊正方形紙片
,折疊正方形紙片![]() ,使
,使![]() 落在
落在![]() 上,點
上,點![]() 恰好與
恰好與![]() 上的點
上的點![]() 重合,展開后,折痕
重合,展開后,折痕![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() ,
,![]() ,連結
,連結![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④四邊形
;④四邊形![]() 是菱形;⑤
是菱形;⑤![]() ,其中正確結論的序號是______.
,其中正確結論的序號是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,M是平行四邊形ABCD的AB邊的中點,CM與BD相交于點E,設平行四邊形ABCD的面積為1,則圖中陰影部分的面積是__________.
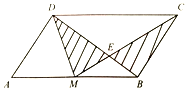
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師隨機抽查了本學期學生讀課外書冊數的情況,繪制成條形圖(圖1)和不完整的扇形圖(圖2),其中條形圖被墨跡遮蓋了一部分.
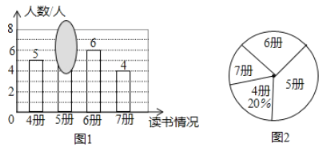
(1)求條形圖中被遮蓋的數,并計算冊數的平均數和中位數;
(2)隨后又補查了另外幾人,得知最少的讀了6冊,將其與之前的數據合并后,發現冊數的中位數沒改變,則最多補查了__________人.從補查結果看,學生的讀書冊數的平均數與之前相比______________.(變大、變小、不變).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的切線,切點為B,OA交⊙O于點C,過點C的切線交AB于點D.若∠BAO=30°,CD=2.
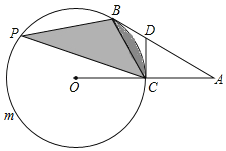
(1)求⊙O的半徑;
(2)若點P在![]() 上運動,設點P到直線BC的距離為x,圖中陰影部分的面積為y,求y與x之間的函數關系式,并寫出自變量x的取值范圍.
上運動,設點P到直線BC的距離為x,圖中陰影部分的面積為y,求y與x之間的函數關系式,并寫出自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某貨車銷售公司,分別試銷售兩種型號貨車各一個月,并從中選擇一種長期銷售,設每月銷售量為x輛若銷售甲型貨車,每月銷售的利潤為y1(萬元),已知每輛甲型貨車的利潤為(m+6)萬元,(m是常數,9≤m≤11),每月還需支出其他費用8萬元,受條件限制每月最多能銷售甲型貨車25輛;若銷售乙型貨車,每月的利潤y2(萬元)與x的函數關系式為y2=ax2+bx-25,且當x=10時,y2=20,當x=20時,y2=55,受條件限制每月最多能銷售乙型貨車40輛.
(1)分別求出y1、y2與x的函數關系式,并確定x的取值范范圍;
(2)分別求出銷售這兩種貨車的最大月利潤;(最大利潤能求值的求值,不能求值的用式子表示)
(3)為獲得最大月利潤,該公司應該選擇銷售哪種貨車?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學活動小組在一次活動中,對一個數學問題作如下探究:
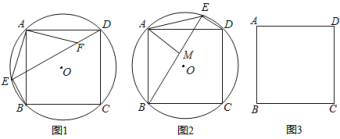
(問題發現)如圖1,正方形ABCD的四個頂點都在⊙O上,若點E在弧AB上,F是DE上的一點,且DF=BE.試說明:△ADF≌△ABE;
(變式探究)如圖2,若點E在弧AD上,過點A作AM⊥BE,請說明線段BE、DE、AM之間滿足等量關系:BE﹣DE=2AM;
(解決問題)如圖3,在正方形ABCD中,CD=2![]() ,若點P滿足PD=2,且∠BPD=90°,請直接寫出點A到BP的距離.
,若點P滿足PD=2,且∠BPD=90°,請直接寫出點A到BP的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com