
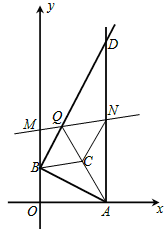
(2013年浙江義烏12分)如圖1,已知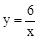 (x>
(x>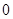 )圖象上一點P,PA⊥x軸于點A(a,0),點B坐標為(0,b)(b>0),動點M是y軸正半軸上B點上方的點,動點N在射線AP上,過點B作AB的垂線,交射線AP于點D,交直線MN于點Q,連結AQ,取AQ的中點為C.
)圖象上一點P,PA⊥x軸于點A(a,0),點B坐標為(0,b)(b>0),動點M是y軸正半軸上B點上方的點,動點N在射線AP上,過點B作AB的垂線,交射線AP于點D,交直線MN于點Q,連結AQ,取AQ的中點為C.

(1)如圖2,連結BP,求△PAB的面積;
(2)當點Q在線段BD上時,若四邊形BQNC是菱形,面積為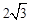 ,求此時P點的坐標;
,求此時P點的坐標;
(3)當點Q在射線BD上時,且a=3,b=1,若以點B,C,N,Q為頂點的四邊形是平行四邊形,求這個平行四邊形的周長.
解:(1)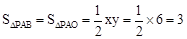 。
。
(2)如圖1,∵四邊形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC。
∵AB⊥BQ,C是AQ的中點,∴BC=CQ=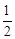 AQ。∴∠BQC=60°,∠BAQ=30°。
AQ。∴∠BQC=60°,∠BAQ=30°。
在△ABQ和△ANQ中,∵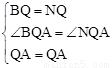 ,∴△ABQ≌△ANQ(SAS)。
,∴△ABQ≌△ANQ(SAS)。
∴∠BAQ=∠NAQ=30°。∴∠BAO=30°。
∵S四邊形BQNC=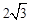 ,∴BQ=2。∴AB=
,∴BQ=2。∴AB=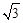 BQ=
BQ=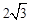 。∴OA=
。∴OA=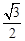 AB=3。
AB=3。
又∵P點在反比例函數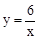 的圖象上,∴P點坐標為(3,2)。
的圖象上,∴P點坐標為(3,2)。
(3)∵OB=1,OA=3,∴AB=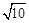 。
。
∵△AOB∽△DBA,∴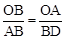 。∴BD=3
。∴BD=3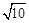 。
。
①如圖2,當點Q在線段BD上,
∵AB⊥BD,C為AQ的中點,∴BC=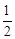 AQ。
AQ。
∵四邊形BNQC是平行四邊形,∴QN=BC,CN=BQ,CN∥BD。
∴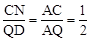 ,∴BQ=CN=
,∴BQ=CN=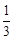 BD=
BD=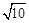 。
。
∴AQ=2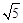 。
。
∴C四邊形BQNC=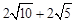 。
。
②如圖3,當點Q在線段BD的延長線上,
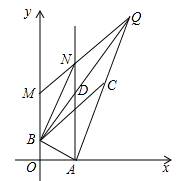
∵AB⊥BD,C為AQ的中點,
∴BC=CQ=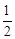 AQ。
AQ。
∴平行四邊形BNQC是菱形,BN=CQ,BN∥CQ。
∴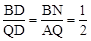 。∴BQ=3BD=9
。∴BQ=3BD=9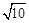 。
。
∴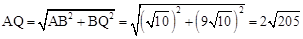 。
。
∴C四邊形BNQC=2AQ=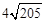 。
。
【解析】(1)根據同底等高的兩個三角形的面積相等即可求出△PAB的面積。
(2)首先求出∠BQC=60°,∠BAQ=30°,然后根據SAS證明△ABQ≌△ANQ,進而求出∠BAO=30°,由S四邊形BQNC=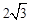 求出OA=3,于是P點坐標求出。
求出OA=3,于是P點坐標求出。
(3)分兩類進行討論,當點Q在線段BD上,根據題干條件求出AQ的長,進而求出四邊形的周長,當點Q在線段考點:反比例函數綜合題,曲線上點的坐標與方程的關系,菱形的性質,全等三角形的判定和性質,相似三角形的判定和性質,勾股定理,分類思想的應用。
BD的延長線上,依然根據題干條件求出AQ的長,再進一步求出四邊形的周長。


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源:2013年初中畢業升學考試(浙江義烏卷)數學(解析版) 題型:解答題
(2013年浙江義烏10分)小明合作學習小組在探究旋轉、平移變換.如圖△ABC,△DEF均為等腰直角三角形,各頂點坐標分別為A(1,1),B(2,2),C(2,1),D( ,0),E(
,0),E( , 0),F(
, 0),F( ,
, ).
).
(1)他們將△ABC繞C點按順時針方向旋轉450得到△A1B1C.請你寫出點A1,B1的坐標,并判斷A1C和DF的位置關系;
(2)他們將△ABC繞原點按順時針方向旋轉450,發現旋轉后的三角形恰好有兩個頂點落在拋物線 上.請你求出符合條件的拋物線解析式;
上.請你求出符合條件的拋物線解析式;
(3)他們繼續探究,發現將△ABC繞某個點旋轉45,若旋轉后的三角形恰好有兩個頂點落在拋物線 上,則可求出旋轉后三角形的直角頂點P的坐標.請你直接寫出點P的所有坐標.
上,則可求出旋轉后三角形的直角頂點P的坐標.請你直接寫出點P的所有坐標.

查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(浙江義烏卷)數學(解析版) 題型:解答題
(2013年浙江義烏10分)為迎接中國森博會,某商家計劃從廠家采購A,B兩種產品共20件,產品的采購單價(元/件)是采購數量(件)的一次函數.下表提供了部分采購數據.
|
采購數量(件) |
1 |
2 |
… |
|
A產品單價(元/件) |
1480 |
1460 |
… |
|
B產品單價(元/件) |
1290 |
1280 |
… |
(1)設A產品的采購數量為x(件),采購單價為y1(元/件),求y1與x的關系式;
(2)經商家與廠家協商,采購A產品的數量不少于B產品數量的 ,且A產品采購單價不低于1200元.求該商家共有幾種進貨方案;
,且A產品采購單價不低于1200元.求該商家共有幾種進貨方案;
(3)該商家分別以1760元/件和1700元/件的銷售單價售出A,B兩種產品,且全部售完.在(2)的條件下,求采購A種產品多少件時總利潤最大,并求最大利潤.
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(浙江義烏卷)數學(解析版) 題型:解答題
(2013年浙江義烏8分)已知直線PD垂直平分⊙O的半徑OA于點B,PD交⊙O于點C,D,PE是⊙O的切線,E為切點,連結AE,交CD于點F.

(1)若⊙O的半徑為8,求CD的長;
(2)證明:PE=PF;
(3)若PF=13,sinA= ,求EF的長.
,求EF的長.
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(浙江義烏卷)數學(解析版) 題型:解答題
(2013年浙江義烏8分)在義烏市中小學生“我的中國夢”讀書活動中,某校對部分學生做了一次主題為“我最喜愛的圖書”的調查活動,將圖書分為甲、乙、丙、丁四類,學生可根據自己的愛好任選其中一類.學校根據調查情況進行了統計,并繪制了不完整的條形統計圖和扇形統計圖.


請你結合圖中信息,解答下列問題:
(1)本次共調查了 名學生;
(2)被調查的學生中,最喜愛丁類圖書的學生有 人,最喜愛甲類圖書的人數占本次被調查人數的 %;
(3)在最喜愛丙類圖書的學生中,女生人數是男生人數的1.5倍.若這所學校共有學生1500人,請你估計該校最喜愛丙類圖書的女生和男生分別有多少人.
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(浙江義烏卷)數學(解析版) 題型:解答題
(2013年浙江義烏6分)如圖1,從邊長為a的正方形紙片中剪去一個邊長為b的小正方形,再沿著線段AB剪開,把剪成的兩張紙片拼成如圖2的等腰梯形.

(1)設圖1中陰影部分面積為S1,圖2中陰影部分面積為S2,請直接用含a,b的代數式表示S1 和S2;
(2)請寫出上述過程所揭示的乘法公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com