
【題目】為豐富學生的文體生活,某校計劃開設五門選修課程:聲樂、足球、舞蹈、書法、演講.要求每名學生必須選修且只能選修一門課程,為保證計劃的有效實施,學校隨機對部分學生進行了一次調查,并將調查結果繪制成如圖不完整的統計圖.請根據統計圖解答下列問題.
(1)本次接受問卷調查的學生有 名;
(2)補全條形統計圖;
(3)扇形統計圖中選修“演講”課程所對應扇形的圓心角的度數為 ;
(4)該校有800名學生,請你估計選修“足球”課程的學生有多少名.
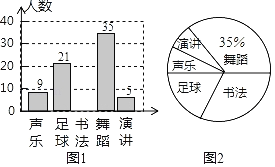
【答案】(1)100;(2)見解析;(3)18°;(4)估計選修“足球”課程的學生有168名.
【解析】
(1)根據舞蹈的人數和所占的百分比即可求出本次接受問卷調查的學生數;
(2)用總人數減去其它課程的人數,求出喜歡書法的人數,從而補全統計圖;
(3)用360°乘以選修“演講”的人數所占的百分比即可;
(4)用該校的總人數乘以選修“足球”人數所占的百分比即可得出答案.
解:(1)本次接受問卷調查的學生有:35÷35%=100(名);
故答案為:100;
(2)喜歡書法的人數有:100﹣9﹣21﹣35﹣5=30(人),
補全統計圖如下:

(3)扇形統計圖中選修“演講”課程所對應扇形的圓心角的度數為:360°×![]() =18°;
=18°;
故答案為:18°;
(4)根據題意得:
800×![]() =168(名),
=168(名),
答:估計選修“足球”課程的學生有168名.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O是坐標原點,拋物線![]() 經過A(-5,0),
經過A(-5,0),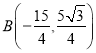 兩點,連接AB,BO.
兩點,連接AB,BO.
(1)求拋物線表達式;
(2)點C是第三象限內的一個動點,若△AOC與△AOB全等,請直接寫出點C坐標______;
(3)若點D從點O出發沿線段OA向點A作勻速運動,速度為每秒1個單位長度,同時線段OA上另一個點H從點A出發沿線段AO向點O作勻速運動,速度為每秒2個單位長度(當點H到達點O時,點D也同時停止運動).過點D作x軸的垂線,與直線OB交于點E,延長DE到點F,使得EF=DE,以DF為邊,在DF左側作等邊三角形DGF(當點D運動時,點G、點F也隨之運動).過點H作x軸的垂線,與直線AB交于點L,延長HL到點M,使得LM=HL,以HM為邊,在HM的右側作等邊三角形HMN(當點H運動時,點M、點N也隨之運動).當點D運動t秒時,△DGF有一條邊所在直線恰好過△HMN的重心,直接寫出此刻t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
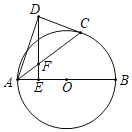
【題目】如圖,AB是⊙O的直徑,點C在半圓上,點D在圓外,DE⊥AB于點E交AC于點F,且DF=CD
(1)求證:CD是⊙O的切線;
(2)若點F是AC的中點,DF=2EF=2![]() ,求⊙O半徑.
,求⊙O半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
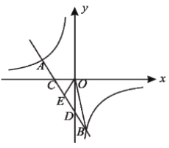
【題目】雙曲線![]() (k為常數,且
(k為常數,且![]() )與直線
)與直線![]() 交于
交于![]() 兩點.
兩點.
(1)求k與b的值;
(2)如圖,直線AB交x軸于點C,交y軸于點D,若點E為CD的中點,求△BOE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
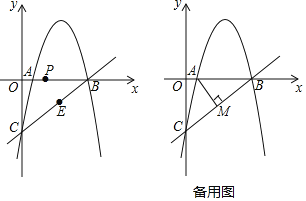
【題目】如圖,拋物線![]() 經過x軸上的點A(1,0)和點B及y軸上的點C,經過B、C兩點的直線為
經過x軸上的點A(1,0)和點B及y軸上的點C,經過B、C兩點的直線為![]() .
.
①求拋物線的解析式.
②點P從A出發,在線段AB上以每秒1個單位的速度向B運動,同時點E從B出發,在線段BC上以每秒2個單位的速度向C運動.當其中一個點到達終點時,另一點也停止運動.設運動時間為t秒,求t為何值時,△PBE的面積最大并求出最大值.
③過點A作![]() 于點M,過拋物線上一動點N(不與點B、C重合)作直線AM的平行線交直線BC于點Q.若點A、M、N、Q為頂點的四邊形是平行四邊形,求點N的橫坐標.
于點M,過拋物線上一動點N(不與點B、C重合)作直線AM的平行線交直線BC于點Q.若點A、M、N、Q為頂點的四邊形是平行四邊形,求點N的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+2x+c與y軸交于點A,與x軸交于點B(3,0)、C(﹣1,0)兩點.
(1)求直線AB和拋物線的表達式;
(2)當點F為直線AB上方拋物線上一動點(不與A、B重合),過點F作FP//x軸交直線AB于點P;過點F作FR//y軸交直線AB于點R,求PR的最大值;
(3)把射線BA繞著點B逆時針旋轉90°得到射線BM,點E在射線BM運動(不與點B重合),以BC、BE為鄰邊作平行四邊形BCDE,點H為DE邊上動點,連接CH,請直接寫出CH+![]() HE的最小值.
HE的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
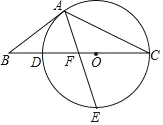
【題目】 如圖,點O在△ABC的BC邊上,⊙O經過點A、C,且與BC相交于點 D.點E是下半圓弧的中點,連接AE交BC于點F,已知AB=BF.
(1)求證:AB是⊙O的切線;
(2)若OC=3,OF=1,求cosB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受疫情影響,某種蔬菜的價格快速上漲,是原價的1.5倍,同樣用48元能買到的蔬菜比原來少了2千克.
(1)求這種蔬菜的原價是每千克多少元?
(2)政府采取增加采購渠道、財政補貼等多種措施,降低特價,方便老百姓的生活.這種蔬菜的批改價兩次下調后,由每千克10元降為每千克6.4元.求平均每次下調的百分率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形![]() 中,
中,![]() 為對角線
為對角線![]() 上任意一點(不與
上任意一點(不與![]() 重合)連接
重合)連接![]() ,過點M作
,過點M作![]() 交
交![]() (或
(或![]() 的延長線)于點
的延長線)于點![]() ,連接
,連接![]() .
.
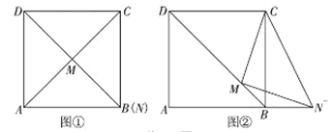
感知:如圖①,當M為![]() 中點時,容易證
中點時,容易證![]() (不用證明);
(不用證明);
探究:如圖②,點M為對角線![]() 上任意一點(不與
上任意一點(不與![]() 重合)請探究
重合)請探究![]() 與
與![]() 的數量關系,并證明你的結論.
的數量關系,并證明你的結論.
應用:(1)直接寫出![]() 的面積S的取值范圍;
的面積S的取值范圍;
(2)若![]() ,則
,則![]() 與
與![]() 的數量關系是_____________.
的數量關系是_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com