
【題目】下表是橘子的銷售額隨橘子賣出質量的變化表:
質量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
銷售額/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)這個表反映了哪兩個變量之間的關系?哪個是自變量?哪個是因變量?
(2)當橘子賣出5千克時,銷售額是_______元.
(3)如果用![]() 表示橘子賣出的質量,
表示橘子賣出的質量,![]() 表示銷售額,按表中給出的關系,
表示銷售額,按表中給出的關系,![]() 與
與![]() 之間的關系式為______.
之間的關系式為______.
(4)當橘子的銷售額是100元時,共賣出多少千克橘子?
【答案】(1)橘子賣出的質量與銷售額之間的關系,橘子賣出的質量是自變量,銷售額是因變量;(2)10;(3)![]() ;(4)共賣出50千克橘子.
;(4)共賣出50千克橘子.
【解析】
(1)根據表格第一列確定變量,再結合自變量和因變量的定義確定自變量與因變量;(2)根據表格解答即可;(3)根據表格可知單價,由單價×數量=總價即可得出y與x的關系式;(4)把y=100代入(3)中的關系式,即可求出銷售橘子數量;
解:(1)橘子賣出的質量與銷售額之間的關系,橘子賣出的質量是自變量,銷售額是因變量;
(2)由表格可知:橘子賣出5千克時,銷售額是10元;
故答案為:10
(3)由表格可知橘子的銷售單價為2元/千克,
∴![]() .
.
故答案為:y=2x
(4)當![]() 時,
時,![]() .
.
答:此時共賣出50千克橘子.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:
【題目】我市某農場有A、B兩種型號的收割機共20臺,每臺A型收割機每天可收大麥100畝或者小麥80畝,每臺B型收割機每天可收大麥80畝或者小麥60畝,該農場現有19 000畝大麥和11 500畝小麥先后等待收割.先安排這20臺收割機全部收割大麥,并且恰好10天時間全部收完.
(1)問A、B兩種型號的收割機各多少臺?
(2)由于氣候影響,要求通過加班方式使每臺收割機每天多完成10%的收割量,問這20臺收割機能否在一周時間內完成全部小麥收割任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在筆直的道路AB上相向而行,甲騎自行車從A地到B地,乙駕車從B地到A地,假設他們分別以不同的速度勻速行駛,甲先出發6分鐘后,乙才出發,在整個過程中,甲、乙兩人之間的距離y(千米)與甲出發的時間x(分)之間的函數圖象如圖.
(1)A地與B地相距______km,甲的速度為______km/分;
(2)求甲、乙兩人相遇時,乙行駛的路程;
(3)當乙到達終點A時,甲還需多少分鐘到達終點B?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:以O為圓心的扇形AOB中,∠AOB=90°,點C為 ![]() 上一動點,射線AC交射線OB于點D,過點D作OD的垂線交射線OC于點E,聯結AE.
上一動點,射線AC交射線OB于點D,過點D作OD的垂線交射線OC于點E,聯結AE.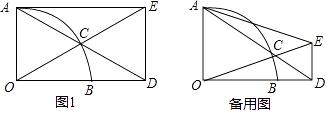
(1)如圖1,當四邊形AODE為矩形時,求∠ADO的度數;
(2)當扇形的半徑長為5,且AC=6時,求線段DE的長;
(3)聯結BC,試問:在點C運動的過程中,∠BCD的大小是否確定?若是,請求出它的度數;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠準備購買A、B兩種零件,已知A種零件的單價比B種零件的單價多30元,而用900元購買A種零件的數量和用600元購買B種零件的數量相等.
(1)求A、B兩種零件的單價;
(2)根據需要,工廠準備購買A、B兩種零件共200件,工廠購買兩種零件的總費用不超過14700元,求工廠最多購買A種零件多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=﹣x+2的圖象與反比例函數y2= ![]() 的圖象相交于A,B兩點,點B的坐標為(2m,﹣m).
的圖象相交于A,B兩點,點B的坐標為(2m,﹣m).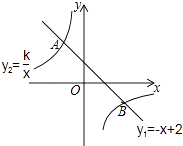
(1)求出m值并確定反比例函數的表達式;
(2)請直接寫出當x<m時,y2的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了創建國家衛生城市,需要購買甲、乙兩種類型的分類垃圾桶替換原來的垃圾桶,![]() ,
,![]() ,
,![]() 三個小區所購買的數量和總價如表所示.
三個小區所購買的數量和總價如表所示.
甲型垃圾桶數量(套) | 乙型垃圾桶數量(套) | 總價(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)問甲型垃圾桶、乙型垃圾桶的單價分別是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com