【題目】下列說法正確的是( )
A. “明天降雨的概率是
”表示明天有的時間降雨
B. “彩票中獎的概率是
”表示買
張彩票一定會中獎
C. “拋一枚硬幣正面朝上的概率是
”表示每拋
次就有
次出現(xiàn)正面朝上
D. “拋一枚普通的正方體骰子，出現(xiàn)朝正面的數(shù)為奇數(shù)的概率是”表示如果這個骰子拋很多很多次，那么平均每次就有次出現(xiàn)朝正面的數(shù)為奇數(shù)
【答案】D
【解析】
A項(xiàng)，“明天降雨的概率是80%”表示明天降雨的可能性為80％，故A項(xiàng)表述錯誤.
B項(xiàng)，彩票中獎的概率是1%，買100張可能中獎也可能不中獎，故B項(xiàng)表述錯誤.
C項(xiàng)，“拋一枚硬幣正面朝上的概率是0.5”表示每拋硬幣2次可能有1次出現(xiàn)正面朝上，故B項(xiàng)表述錯誤.
D項(xiàng)，在相同條件下重復(fù)進(jìn)行的n次試驗(yàn)中，事件A發(fā)生的頻率穩(wěn)定地在某一常數(shù)p附近擺動，且隨n越大擺動幅度越小，則稱p為事件A的概率，當(dāng)大量重復(fù)拋擲骰子時，向上一面的點(diǎn)數(shù)為奇數(shù)發(fā)生的頻率接近于概率，平均每拋2次就有1次向上一面的點(diǎn)數(shù)為奇數(shù)，故D項(xiàng)表述正確.
根據(jù)分析可得，答案選D.
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，
是直角三角形，
，
，以點(diǎn)
為旋轉(zhuǎn)中心，將旋轉(zhuǎn)到
的位置，且使
經(jīng)過點(diǎn)
．
求
的度數(shù)，判斷
的形狀；
求線段
與線段
的數(shù)量關(guān)系．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】
（1）如圖1，在正方形ABCD中，M是BC邊（不含端點(diǎn)B、C）上任意一點(diǎn)，P是BC延長線上一點(diǎn)，N是∠DCP的平分線上一點(diǎn)．若∠AMN=90°，求證：AM=MN．
下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
證明：在邊AB上截取AE=MC，連ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．
（下面請你完成余下的證明過程）
（2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2），N是∠ACP的平分線上一點(diǎn)，則當(dāng)∠AMN=60°時，結(jié)論AM=MN是否還成立？請說明理由．
（3）若將（1）中的“正方形ABCD”改為“正
邊形ABCD……X”，請你作出猜想：當(dāng)∠AMN= °時，結(jié)論AM=MN仍然成立．（直接寫出答案，不需要證明）
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，扇形OMN的圓心角為45°，正方形A1B1C1A2的邊長為2，頂點(diǎn)A1，A2在線段OM上，頂點(diǎn)B1在弧MN上，頂點(diǎn)C1在線段ON上，在邊A2C1上取點(diǎn)B2，以A2B2為邊長繼續(xù)作正方形A2B2C2A3，使得點(diǎn)C2在線段ON上，點(diǎn)A3在線段OM上，……，依次規(guī)律，繼續(xù)作正方形，則A2018M=__________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知∠1=∠2，則下列條件中不一定能使△ABC≌△ABD的是( )
A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知：如圖，∠ACB=∠ADB=90°，E為AB中點(diǎn)，連接DE、CE、CD．
（1）求證：DE=CE；
（2）若∠CAB=25°，∠DBA=35°，判斷△DEC的形狀，并說明理由；
（3）當(dāng)∠CAB+∠DBA=45°時，若CD=12，取CD中點(diǎn)F，求EF的長．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知：在
中，
，
，
，動點(diǎn)
從點(diǎn)
出發(fā)，以每秒
個單位的速度沿
方向向終點(diǎn)
運(yùn)動；同時，動點(diǎn)
也從點(diǎn)出發(fā)，以每秒
個單位的速度沿
方向向終點(diǎn)
運(yùn)動．設(shè)兩點(diǎn)運(yùn)動的時間為
秒
．
連接
，在點(diǎn)、運(yùn)動過程中，
與是否始終相似？請說明理由；
連接
，設(shè)
的面積為
，求關(guān)于的函數(shù)關(guān)系式；
連接、
，是否存在的值，使
？若存在，求出的值；若不存在，請說明理由；
探索：把
沿直線折疊成
，設(shè)
與交于點(diǎn)
，當(dāng)
是直角三角形時，請直接寫出的值．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】某品牌化妝品商店有
、
、
三種型號的化妝品，今年國慶節(jié)期間采用組合打折銷售，銷售時采用了三種組合的方式進(jìn)行銷售，甲種組合是：
盒種，盒 種，
盒 種；乙種組合是：
盒 種，
盒種；丙種組合是：
盒 種，
盒種，盒種.如果組合銷售打折后A種每盒售價為
元， 種每盒售價為
元， 種每盒售價為
元.國慶節(jié)當(dāng)天，商店采用三種組合搭配的方式進(jìn)行銷售后共得銷售額為
元，其中 種的銷售額為
元，那么種化妝品的銷售額是______．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
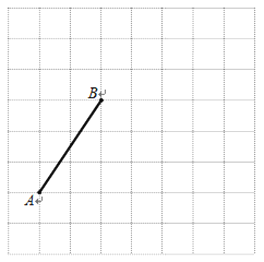
【題目】下圖是由邊長為1個單位長度的小正方形組成的網(wǎng)格，線段AB的端點(diǎn)在格點(diǎn)上.
（1）請建立適當(dāng)?shù)钠矫嬷苯亲鴺?biāo)系xOy，使得A點(diǎn)的坐標(biāo)為（-3，-1），在此坐標(biāo)系下，B點(diǎn)的坐標(biāo)為________________；
（2）將線段BA繞點(diǎn)B逆時針旋轉(zhuǎn)90°得線段BC，畫出BC；在第(1)題的坐標(biāo)系下，C點(diǎn)的坐標(biāo)為__________________；
（3）在第(1)題的坐標(biāo)系下，二次函數(shù)y=ax2+bx+c(a≠０)的圖象過O、B、C三點(diǎn)，則此函數(shù)圖象的對稱軸方程是________________.
【答案】 （-1，2） （2，0） x=1
【解析】分析：
根據(jù)點(diǎn)
的坐標(biāo)建立坐標(biāo)系，即可寫出點(diǎn)
的坐標(biāo).
畫出點(diǎn)旋轉(zhuǎn)后的對應(yīng)點(diǎn)
連接
,寫出點(diǎn)
的坐標(biāo).
用待定系數(shù)法求出函數(shù)解析式，即可求出對稱軸方程.
詳解：（1）建立坐標(biāo)系如圖，
B點(diǎn)的坐標(biāo)為
；
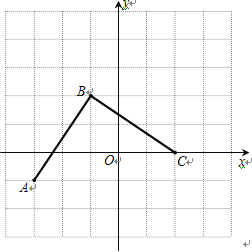
（2）線段BC如圖，C點(diǎn)的坐標(biāo)為
（3）把點(diǎn)
代入二次函數(shù)
，得
解得：
二次函數(shù)解析為：
對稱軸方程為：
故對稱軸方程是
點(diǎn)睛：考查圖形與坐標(biāo)；旋轉(zhuǎn)、對稱變換；待定系數(shù)法求二次函數(shù)解析式，二次函數(shù)的圖象與性質(zhì).熟練掌握各個知識點(diǎn)是解題的關(guān)鍵.
【題型】解答題
【結(jié)束】
18
【題目】特殊兩位數(shù)乘法的速算——如果兩個兩位數(shù)的十位數(shù)字相同，個位數(shù)字相加為10，那么能立說出這兩個兩位數(shù)的乘積.如果這兩個兩位數(shù)分別寫作AB和AC（即十位數(shù)字為A，個位數(shù)字分別為B、C，B+C=10，A>3），那么它們的乘積是一個4位數(shù)，前兩位數(shù)字是A和(A+1)的乘積，后兩位數(shù)字就是B和C的乘積.
如：47×43=2021，61×69=4209.
（1）請你直接寫出83×87的值；
（2）設(shè)這兩個兩位數(shù)的十位數(shù)字為x(
（3）99991×99999=___________________（直接填結(jié)果）
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com