
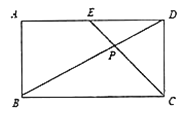
【題目】學完《平面直角坐標系》和《一次函數》這兩章后,老師布置了這樣一道思考題:已知:如圖,在長方形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,
的中點,![]() 和
和![]() 相交于點
相交于點![]() .求
.求![]() 的面積.小明同學應用所學知識,順利地解決了此題,他的思路是這樣的:以
的面積.小明同學應用所學知識,順利地解決了此題,他的思路是這樣的:以![]() 所在的直線為
所在的直線為![]() 軸,以
軸,以![]() 所在的直線為
所在的直線為![]() 軸建立適當的平面直角坐標系,寫出圖中一些點坐標.根據一次函數的知識求出點
軸建立適當的平面直角坐標系,寫出圖中一些點坐標.根據一次函數的知識求出點![]() 的坐標,從而求得
的坐標,從而求得![]() 的面積.請你按照小明的思路解決這道思考題.
的面積.請你按照小明的思路解決這道思考題.
【答案】![]()
【解析】
以點B為原點、BC所在的直線為x軸、BA所在的直線為y軸建立直角坐標系,由此可得出點B、A、C、E、D的坐標,利用待定系數法即可得出直線BD、CE的解析式,聯(lián)立兩直線解析式成方程組,解之即可得出點P的坐標,再根據三角形的面積公式即可求出△BPC的面積.
解:如圖建立直角坐標系,
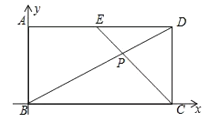
則點B(0,0)、C(4,0)、A(0,2)、D(4,2)、E(2,2).
設直線BD的解析式為y=kx,
將點D(4,2)代入y=kx,得2=4k,
解得:k=![]() ,
,
∴直線BD的解析式為y=![]() x;
x;
設直線CE的解析式為y=mx+n,
將點C(4,0),E(2,2)代入y=mx+n,得![]() ,
,
解得:![]() ,
,
∴直線CE的解析式為y=x+4,
聯(lián)立直線BD、CE的解析式成方程組 ,
,
解得:![]() ,
,
∴點P的坐標為(![]() ,
,![]() ),
),
∴S△BPC=![]() BCyP=
BCyP=![]() ×4×
×4×![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 的位置如圖所示(每個小方格都是邊長1個單位長度的正方形).
的位置如圖所示(每個小方格都是邊長1個單位長度的正方形).
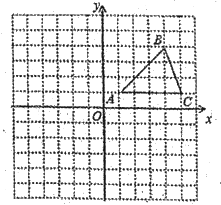
(1)將![]() 沿
沿![]() 軸方向向左平移6個單位,畫出平移后得到的
軸方向向左平移6個單位,畫出平移后得到的![]() .
.
(2)將![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() ,畫出旋轉后得到的
,畫出旋轉后得到的![]() ;直接寫出點
;直接寫出點![]() 的坐標.
的坐標.
(3)作出![]() 關于原點
關于原點![]() 成中心對稱的
成中心對稱的![]() ,并直接寫出
,并直接寫出![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點O在直線MN上,過點O作射線OP,使∠MOP=130°,將一塊直角三角板的直角頂點始終放在點O處.
(1)如圖①,當三角板的一邊OA在射線OM上,另一邊OB在直線MN的上方時,求∠POB的度數;
(2)若將三角板繞點O旋轉至圖②所示的位置,此時OB恰好平分∠PON,求∠BOP和∠AOM 的度數;
(3)若將三角板繞點O旋轉至圖③所示位置,此時OA在∠PON 的內部,若OP所在的直線平分∠MOB,求∠POA 的度數;
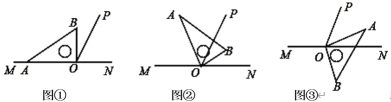
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的三個頂點的位置如圖所示,將△ABC水平向左平移3個單位,再豎直向下平移2個單位。
(1)讀出△ABC的三個頂點坐標;
(2)請畫出平移后的△A′B′C′,并直接寫出點A/、B′、C′的坐標;
(3)求平移以后的圖形的面積 。
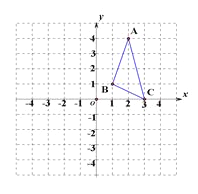
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形ABCD中,AB=6,BC=8.點P在矩形ABCD的內部,點E在邊BC上,滿足△PBE∽△DBC,若△APD是等腰三角形,則PE的長為數___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“中國夢”是中華民族每一個人的夢,也是每一個中小學生的夢,各中小學開展經典誦讀活動,無疑是“中國夢”教育這一宏大樂章里的響亮音符,學校在經典誦讀活動中,對全校學生用A、B、C、D四個等級進行評價,現從中抽取若干個學生進行調查,繪制出了兩幅不完整的統(tǒng)計圖,請你根據圖中信息解答下列問題:
(1)共抽取了多少個學生進行調查?
(2)將圖甲中的折線統(tǒng)計圖補充完整.
(3)求出圖乙中B等級所占圓心角的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校招生時,2640名學生的成績數據分別由兩位程序操作員各向計算機輸入一遍,已知甲的輸入速度是乙的2倍,結果甲比乙少用2小時輸完.問這兩個操作員每分鐘各能輸入多少名學生的成績?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,與BC相交于點F,過點B作BE⊥AD于點D,交AC延長線于點E,過點C作CH⊥AB于點H,交AF于點G,則下列結論:![]() ⑤
⑤![]() ;正確的有( )個.
;正確的有( )個.
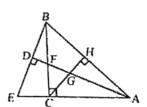
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)如圖,某數學活動小組為測量學校旗桿AB的高度,從旗桿正前方2![]() m處的點C出發(fā),沿斜面坡度i=1∶
m處的點C出發(fā),沿斜面坡度i=1∶![]() 的斜坡CD前進4m到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5 m.已知A,B,C,D,E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈
的斜坡CD前進4m到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5 m.已知A,B,C,D,E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,計算結果保留根號)
,計算結果保留根號)
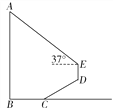
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com