
【題目】我們知道,任意一個正整數![]() 都可以進行這樣的分解,
都可以進行這樣的分解,![]() (
(![]() ,
,![]() 是正整數且
是正整數且![]() ),在
),在![]() 的所有這種分解中,如果
的所有這種分解中,如果![]() ,
,![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是
是![]() 的最佳分解,并規定:
的最佳分解,并規定:![]() ,例如
,例如![]() 可以分解成
可以分解成![]() 、
、![]() 或
或![]() .因為
.因為![]() ,所有
,所有![]() 是最佳分解,所以
是最佳分解,所以![]() .
.
(1)求![]() .
.
(2)如果一個兩位正整數![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為
為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為![]() ,那么我們稱這個數
,那么我們稱這個數![]() 為 “吉祥數”,求所有“吉祥數”中
為 “吉祥數”,求所有“吉祥數”中![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先將24分解,得到其最佳分解,則按![]() 可得答案;
可得答案;
(2)根據“吉祥數”定義知(10y+x)-(10x+y)=18,即y=x+2,結合x的范圍可得2位數的“吉祥數”,求出每個“吉祥數”F(t)的值后比較大小即可.
(1)∵24=1×24=2×12=3×8=4×6
24-1>12-2>8-3>6-4
∴F(24)=![]()
(2)設交換t的個位上的數與十位上的數得到的新數為t′,則t′=10y+x,
∵t為“吉祥數”,
∴t′-t=(10y+x)-(10x+y)=9(y-x)=18,
∴y=x+2,
∵1≤x≤y≤9,x,y為自然數,
∴“吉祥數”有:13,24,35,46,57,68,79,
∴所有“吉祥數”中F(t)的值為:F(13)=![]() ,F(24)=
,F(24)=![]() ,F(35)=
,F(35)=![]() ,F(46)=
,F(46)=![]() ,F(57)=
,F(57)=![]() ,F(68)=
,F(68)=![]() ,F(79)=
,F(79)=![]() .
.
∵![]() ,
,
∴所有“吉祥數”中,F(t)的最大值是![]() .
.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】請僅用無刻度的直尺完成下列畫圖,不寫畫法,保留畫圖痕跡.(用虛線表示畫圖過程,實線表示畫圖結果)
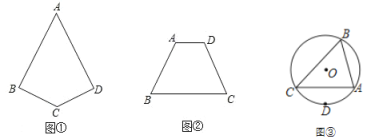
(1)如圖①,四邊形 ABCD 中,AB=AD,∠B=∠D,畫出四邊形 ABCD 的對稱軸 m;
(2)如圖②,四邊形 ABCD 中,AD∥BC,∠A=∠D,畫出 BC 邊的垂直平分線 n.
(3)如圖③,△ABC 的外接圓的圓心是點 O,D 是![]() 的中點,畫一條直線把△ABC 分成面積相等的兩部分.
的中點,畫一條直線把△ABC 分成面積相等的兩部分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的外接圓為⊙O,AD是⊙O的直徑,過點B作⊙O的切線,交DA的延長線于點E,連接BD,且∠E=∠DBC.
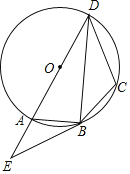
(1)求證:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(t,1)為函數y=ax2+bx+4(a,b為常數,且a≠0)與y=x圖象的交點.
(1)求t;
(2)若函數y=ax2+bx+4的圖象與x軸只有一個交點,求a,b;
(3)若1≤a≤2,設當![]() ≤x≤2時,函數y=ax2+bx+4的最大值為m,最小值為n,求m﹣n的最小值.
≤x≤2時,函數y=ax2+bx+4的最大值為m,最小值為n,求m﹣n的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一個自然數所有數位上的數字先平方再求和得到一個新數,叫做第一次運算,再把所得新數所有數位上的數字先平方再求和又將得到一個新數,叫做第二次運算,……如此重復下去,若最終結果為1,我們把具有這種特征的自然數稱為“快樂數”.例如:
![]() ,
,
![]() ,
,
所以32和70都是“快樂數”.
(1)寫出最小的兩位“快樂數”;判斷19是不是“快樂數”;并說明理由;
(2)若一個三位“快樂數”經過兩次運算后結果為1,把這個三位“快樂數”與它的各位上的數字相加所得的和被8除余數是2,求出這個“快樂數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D,E,F分別是△ABC三邊的中點,則下列判斷錯誤的是( )
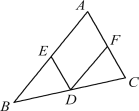
A. 四邊形AEDF一定是平行四邊形 B. 若AD平分∠A,則四邊形AEDF是正方形
C. 若AD⊥BC,則四邊形AEDF是菱形 D. 若∠A=90°,則四邊形AEDF是矩形
查看答案和解析>>
科目:初中數學 來源: 題型:
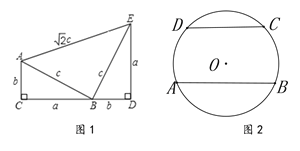
【題目】如圖1,四邊形ACDE是美國第二十任總統伽菲爾德驗證勾股定理時用到的一個圖形,a,b,c是Rt△ABC和Rt△BED邊長,易知AE=![]() ,這時我們把關于x的形如
,這時我們把關于x的形如![]() 的一元二次方程稱為“勾系一元二次方程”.
的一元二次方程稱為“勾系一元二次方程”.
請解決下列問題:
(1)判斷方程![]() 是否是 “勾系一元二次方程”;并說明理由.
是否是 “勾系一元二次方程”;并說明理由.
(2)求證:關于![]() 的“勾系一元二次方程”
的“勾系一元二次方程” ![]() 必有實數根;
必有實數根;
(3)如圖2,已知AB、CD是半徑為5的⊙O的兩條平行弦,AB=2a,CD=2b,a≠b,關于x的方程![]() 是“勾系一元二次方程”,求∠BAC的度數
是“勾系一元二次方程”,求∠BAC的度數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com