
【題目】△ABC中,AC=BC,∠ACB=α,點D是平面內不與點A和點B重合的一點,連接DB,將線段DB繞點D順時針旋轉α得到線段DE,連接AE、BE、CD.
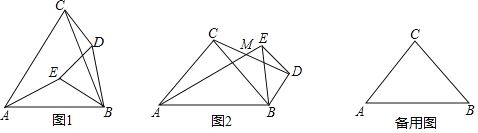
(1)如圖①,點D與點A在直線BC的兩側,α=60°時,![]() 的值是 ;直線AE與直線CD相交所成的銳角的度數是 度;
的值是 ;直線AE與直線CD相交所成的銳角的度數是 度;
(2)如圖②,點D與點A在直線BC兩側,α=90°時,求![]() 的值及直線AE與直線CD相交所成的銳角∠AMC的度數;
的值及直線AE與直線CD相交所成的銳角∠AMC的度數;
(3)當α=90°,點D在直線AB的上方,S△ABD=![]() S△ABC,請直接寫出當點C、D、E在同一直線上時,
S△ABC,請直接寫出當點C、D、E在同一直線上時,![]() 的值.
的值.
【答案】(1)1,60;(2)∠AMC=45°;(3)![]() 的值為2﹣
的值為2﹣![]() 或2+
或2+![]() .
.
【解析】
(1)延長AE,CD交于點H,根據旋轉的性質可知DE=BD,∠BDE=60°,從而可知△BDE,從而可證△ABE≌△CBD,從而可知![]() ,再根據角的關系即可求出∠AHB;
,再根據角的關系即可求出∠AHB;
(2)先證△ABE∽△CBD,可以得到![]() ,∠BAE=∠BCD,繼而可以求出∠AMC的度數;
,∠BAE=∠BCD,繼而可以求出∠AMC的度數;
(3)分兩種情況討論即可:①點D,點A在直線BC兩側,②點A,點D在直線BC同側.
(1)如圖1,延長AE,CD交于點H,
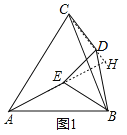
∵將線段DB繞點D順時針旋轉α得到線段DE,
∴DE=BD,∠BDE=60°,
∴△BDE是等邊三角形,
∴BD=BE,∠DBE=60°,
∵△ABC是等邊三角形,
∴AB=BC,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,且BE=BD,AB=BC,
∴△ABE≌△CBD(SAS)
∴AE=CD,∠DCB=∠BAE,
∴![]() =1,
=1,
∵∠BAC+∠ACB=120°,
∴∠BAE+∠CAE+∠ACB=120°,
∴∠CAE+∠ACB+∠BCD=120°
∴∠CAE+ACH=120°,
∴∠AHB=60°,
故答案為:1,60.
(2)∵AC=BC,∠ACB=90°,
∴AB=![]() BC,∠ABC=45°,
BC,∠ABC=45°,
∵將線段DB繞點D順時針旋轉90°得到線段DE,
∴DE=BD,∠BDE=90°,
∴BE=![]() BD,∠DBE=45°,
BD,∠DBE=45°,
∴∠DBE=∠ABC,
∴∠ABE=∠CBD,且![]() ,
,
∴△ABE∽△CBD,
∴![]() ,∠BAE=∠BCD,
,∠BAE=∠BCD,
∵∠BAC+∠ACB=135°=∠ACB+∠CAM+∠BAE,
∴∠ACB+∠CAM+∠BCD=∠CAM+∠ACM=135°,
∴∠AMC=45°;
(3)①若點D,點A在直線BC兩側,如圖3,分別取AC,BC中點G,H,連接GH,
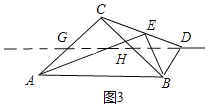
∵![]() ,
,
∴點D在直線GH上,
∵∠ACB=∠BDE=90°,AC=BC,DE=BD,
∴∠CAB=∠CBA=45°,∠DEB=∠DBE=45°,BE=![]() BD,
BD,
∵點G,點H分別是AC,BC的中點,
∴GH∥AB,
∴∠DHB=∠ABC=45°,
∵點C、E、D三點共線,
∴∠CDB=90°,且點H是BC中點,
∴DH=CH=BH,
∴∠HCD=∠HDC,且∠HCD+∠HDC=∠BHD=45°,
∴∠HCD=∠HDC=22.5°,
∵∠BED=∠BCE+∠CBE=45°,
∴∠BCE=∠CBE=22.5°,
∴BE=CE=![]() BD,
BD,
∴CD=CE+DE=(![]() +1)BD,
+1)BD,
∴![]() ;
;
②若點A,點D在直線BC同側,如圖4,分別取AC,BC中點G,H,連接GH,
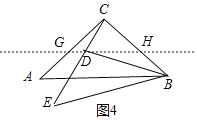
∵![]() ,
,
∴點D在直線GH上,
∵∠ACB=∠BDE=90°,AC=BC,DE=BD,
∴∠CAB=∠CBA=45°,∠DEB=∠DBE=45°,BE=![]() BD,
BD,
∵點G,點H分別是AC,BC的中點,
∴GH∥AB,
∴∠DHC=∠ABC=45°,
∵點C、E、D三點共線,
∴∠CDB=90°,且點H是BC中點,
∴DH=CH=BH,
∴∠HBD=∠HDB,且∠HBD+∠HDB=∠CHD=45°,
∴∠HBD=∠HDB=22.5°,
∵∠ECB=67.5°,∠EBC=∠EBD+∠DBC=67.5°,
∴∠BCE=∠CBE=67.5°,
∴BE=CE=![]() BD,
BD,
∴CD=CE﹣DE=(![]() ﹣1)BD,
﹣1)BD,
∴![]() ,
,
綜上所述:![]() 的值為
的值為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中裝有4個分別標有數1,2,3,4的小球,它們的形狀、大小完全相同,小紅先從口袋里隨機摸出一個小球記下數為x,小穎在剩下的3個球中隨機摸出一個小球記下數為y,這樣確定了點P的坐標(x,y).
(1)小紅摸出標有數3的小球的概率是多少?.
(2)請你用列表法或畫樹狀圖法表示出由x,y確定的點P(x,y)所有可能的結果.
(3)求點P(x,y)在函數y=﹣x+5圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
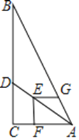
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,點D在邊BC上,點E在線段AD上,EF⊥AC于點F,EG⊥EF交AB于點G.若EF = EG,則CD的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于點G,連接AF,給出下列結論:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四邊形CEGF=S△ABG,其中正確的個數為( )
GE; ④S四邊形CEGF=S△ABG,其中正確的個數為( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,BC=5,點E在AD邊上且不與點A和點D重合,點O是對角線BD的中點,當△OED是等腰三角形時,AE的長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O交AB于點D,過點D作⊙O的切線交BC于點E,連接OE
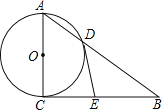
(1)求證:△DBE是等腰三角形
(2)求證:△COE∽△CAB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平面圖形S,點P、Q是S上任意兩點,我們把線段PQ的長度的最大值稱為平面圖形S的“寬距”.例如,正方形的寬距等于它的對角線的長度.
(1)寫出下列圖形的寬距:
①半徑為1的圓: ;
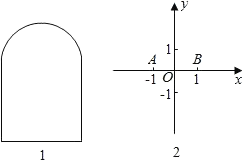
②如圖1,上方是半徑為1的半圓,下方是正方形的三條邊的“窗戶形“: ;
(2)如圖2,在平面直角坐標系中,已知點A(﹣1,0)、B(1,0),C是坐標平面內的點,連接AB、BC、CA所形成的圖形為S,記S的寬距為d.
①若d=2,求點C所在的區域的面積;
②若點C在⊙M上運動,⊙M的半徑為1,圓心M在過點(0,2)且與y軸垂直的直線上.對于⊙M上任意點C,都有5≤d≤8,直接寫出圓心M的橫坐標x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
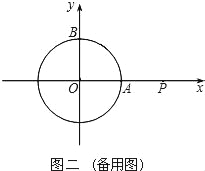
【題目】以坐標原點為圓心,1為半徑的圓分別交x,y軸的正半軸于點A,B.
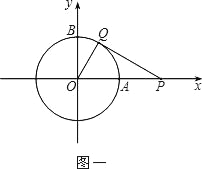
(1)如圖一,動點P從點A處出發,沿x軸向右勻速運動,與此同時,動點Q從點B處出發,沿圓周按順時針方向勻速運動.若點Q的運動速度比點P的運動速度慢,經過1秒后點P運動到點(2,0),此時PQ恰好是⊙O的切線,連接OQ.求∠QOP的大小;
(2)若點Q按照(1)中的方向和速度繼續運動,點P停留在點(2,0)處不動,求點Q再經過5秒后直線PQ被⊙O截得的弦長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點P為圓上一點,點C為AB延長線上一點,PA=PC,∠C=30°.
(1)求證:CP是⊙O的切線.
(2)若⊙O的直徑為8,求陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com