
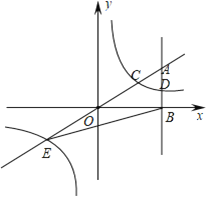
【題目】如圖,在平面直角坐標系中,A點的坐標為(a,6),AB⊥x軸于點B,![]() =
=![]() ,反比例函數y=
,反比例函數y=![]() 的圖象的一支分別交AO、AB于點C、D.延長AO交反比例函數的圖象的另一支于點E.已知點D的縱坐標為
的圖象的一支分別交AO、AB于點C、D.延長AO交反比例函數的圖象的另一支于點E.已知點D的縱坐標為![]() .
.
(1)求反比例函數的解析式及點E的坐標;
(2)連接BC,求S△CEB.
(3)若在x軸上的有兩點M(m,0)N(-m,0).
①以E、M、C、N為頂點的四邊形能否為矩形?如果能求出m的值,如果不能說明理由.
②若將直線OA繞O點旋轉,仍與y=![]() 交于C、E,能否構成以E、M、C、N為頂點的四邊形為菱形,如果能求出m的值,如果不能說明理由.
交于C、E,能否構成以E、M、C、N為頂點的四邊形為菱形,如果能求出m的值,如果不能說明理由.
【答案】(1)反比例函數的解析式為:y=![]() ;E(-4,-3);(2)24;(3)①m=5或-5.②以E、M、C、N為頂點的四邊形不能為菱形.
;E(-4,-3);(2)24;(3)①m=5或-5.②以E、M、C、N為頂點的四邊形不能為菱形.
【解析】
(1)根據已知條件可求A、D的坐標,用待定系數法即求出反比例函數解析式;由點A坐標求直線OA的解析式,把直線OA與反比例函數解析式聯立方程組,即求出交點E;
(2)把△CEB分成△COB與△EOB,以OB為公共底,點C和點E縱坐標的絕對值為高即求出三角形面積;
(3)先由OC=OE,OM=ON得四邊形EMCN為平行四邊形.①若為矩形,則對角線相等,即MN=CE,易求出m的值;②若為菱形,則對角線互相垂直,但CE不與x軸垂直,矛盾,故不能成為菱形.
本題考查了反比例函數的圖象與性質,反比例函數與一次函數的綜合運用,平行四邊形、矩形、菱形的判定.
(1)∵A點的坐標為(a,6),AB⊥x軸于B,
∴AB=6,
∵![]() ,
,
∴OB=8,
∴A(8,6),D(8,![]() ),
),
∵點D在反比例函數y=![]() 的圖象上,
的圖象上,
∴k=8×![]() =12,
=12,
∴反比例函數的解析式為:y=![]() ,
,
設直線OA的解析式為:y=bx,
∴8b=6,解得:b=![]() ,
,
∴直線OA的解析式為:y=![]() x,
x,
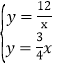 解得:
解得:![]() ,
,![]() ,
,
∴E(-4,-3);
(2)由(1)可知C(4,3),E(-4,-3),B(8,0),
∴S△CEB=S△COB+S△EOB=![]() =
=![]() OB(yC+|yE|)=
OB(yC+|yE|)=![]() ×8×(3+3)=24;
×8×(3+3)=24;
(3)①以E、M、C、N為頂點的四邊形能為矩形,
∵M(m,0),N(-m,0),
∴OM=ON,
∵
∴四邊形EMCN是平行四邊形,
當MN=CE=2OC=2×![]() =10時,EMCN為矩形,
=10時,EMCN為矩形,
∴OM=ON=5,
∴m=5或-5;
②∵CE所在直線OA不可能與x軸垂直,即CE不能與MN垂直,
∴以E、M、C、N為頂點的四邊形不能為菱形.


科目:初中數學 來源: 題型:
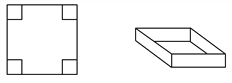
【題目】用一塊邊長為60cm的正方形薄鋼片制作一個長方體盒子.
(1)如果要做成一個沒有蓋的長方體盒子,可先在薄鋼片的四個角上截去四個相同的小正方形,然后把四邊折合起來(如圖所示).設小正方形的邊長為xcm,當做成盒子的底面積為900cm2時,求該盒子的高;
(2)如果要做成一個有蓋的長方體盒子,其制作方案要求同時符合下列兩個條件:
①必須在薄鋼片四個角上各截去一個四邊形(其余部分不能裁截);
②折合后薄鋼片既無空隙又不重疊地圍成各盒面.
請你畫出符合上述制作方案的一種草圖,并求當底面積為800cm2時,該盒子的高.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c的頂點為M(﹣2,﹣4),與x軸交于A、B兩點,且A(﹣6,0),與y軸交于點C.
(1)求拋物線的函數解析式;
(2)求△ABC的面積;
(3)能否在拋物線第三象限的圖象上找到一點P,使△APC的面積最大?若能,請求出點P的坐標;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
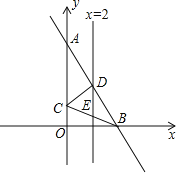
【題目】如圖,平面直角坐標系中,直線AB:y=-2x+8交y軸于點A,交x軸于點B,以AB為底作等腰三角形△ABC的頂點C恰好落在y軸上,連接BC,直線x=2交AB于點D,交BC于點E,交x軸于點G,連接CD.
(1)求證:∠OCB=2∠CBA;
(2)求點C的坐標和直線BC的解析式;
(3)求△DEB的面積;
(4)在x軸上存在一點P使PD-PC最長,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商廈進貨員預測一種應季襯衫能暢銷市場,就用10000元購進這種襯衫,面市后果然供不應求.于是,商廈又用22000元購進了第二批這種襯衫,所購數量是第一批購進數量的2倍,但單價貴了4元,商廈銷售這種襯衫時每件預定售價都是58元.
(1)求這種襯衫原進價為每件多少元?
(2)經過一段時間銷售,根據市場飽和情況,商廈經理決定對剩余的100件襯衫進行打折銷售,以提高回款速度,要使這兩批襯衫的總利潤不少于8600元,最多可以打幾折?
查看答案和解析>>
科目:初中數學 來源: 題型:
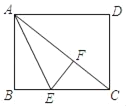
【題目】如圖,矩形紙片ABCD中,已知AD=12,AB=9,E是BC上的點,以AE為折痕折疊紙片,使點B落在點F處,連接FC,當△EFC為直角三角形時,BE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在荔枝種植基地有A、B兩個品種的樹苗出售,已知A種比B種每株多20元,買1株A種樹苗和2株B種樹苗共需200元.
(1)問A、B兩種樹苗每株分別是多少元?
(2)為擴大種植,某農戶準備購買A、B兩種樹苗共36株,且A種樹苗數量不少于B種數量的一半,請求出費用最省的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了促進學生多樣化發展,某校組織開展了社團活動,分別設置了體育類、藝術類、文學類及其它類社團(要求人人參與社團,每人只能選擇一項).為了解學生喜愛哪種社團活動,學校做了一次抽樣調查.根據收集到的數據,繪制成如下兩幅不完整的統計圖,請根據圖中提供的信息,完成下列問題:
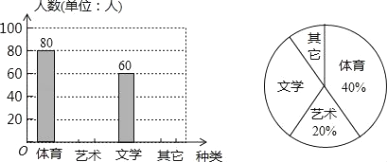
(1)此次共調查了多少人?
(2)求文學社團在扇形統計圖中所占圓心角的度數;
(3)請將條形統計圖補充完整;
(4)若該校有1500名學生,請估計喜歡體育類社團的學生有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com