

 ;
;

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:不詳 題型:解答題
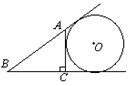
 直徑AB是河底線,弦CD是水位線,CD∥AB,且CD =" 24"
直徑AB是河底線,弦CD是水位線,CD∥AB,且CD =" 24"  m.已測得水面距橋洞最高處有8m
m.已測得水面距橋洞最高處有8m 中點到CD的距離)
中點到CD的距離)
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.7cm | B.17cm | C.12cm | D.7cm或17cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com