
 AC+CB
AC+CB
 ×6+8
×6+8 CB+AC
CB+AC ×8+6
×8+6

 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:單選題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 方向行進200米到點C處,測得B在點C的南偏西60° 的方向上,他們測得東江的寬度是多少米?(結果保留整數,參考數據:
方向行進200米到點C處,測得B在點C的南偏西60° 的方向上,他們測得東江的寬度是多少米?(結果保留整數,參考數據: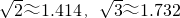 )
)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com