
【題目】在△ABC中,AB=AC=5,sinB=![]() ,⊙O過點B、C兩點,且⊙O半徑r=
,⊙O過點B、C兩點,且⊙O半徑r=![]() ,則OA的長為_____.
,則OA的長為_____.
【答案】3或5
【解析】
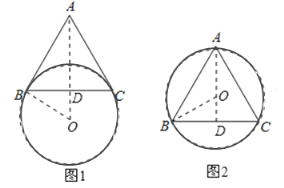
作AD⊥BC于D,由于AB=AC=5,根據等腰三角形的性質得AD垂直平分BC,根據垂徑定理的推論得到點O在直線AD上,連結OB,在Rt△ABD中,根據正弦的定義計算出AD=4,根據勾股定理計算出BD=3,再在Rt△OBD中,根據勾股定理計算出OD=1,然后分類討論:①當點A與點O在BC的兩側,有OA=AD+OD;②當點A與點O在BC的同側,有OA=AD﹣OD,即求得OA的長.
解:如圖,作AD⊥BC于D,
∵AB=AC=5,
∴AD垂直平分BC,
∴點O在直線AD上,
連結OB,
在Rt△ABD中,sin∠ABD=![]() =
=![]() ,
,
∵AB=5,∴AD=4,
∴BD=![]() =
=![]() =3,
=3,
在Rt△OBD中,OB=![]() ,BD=3,
,BD=3,
∴OD=![]() =1,
=1,
當點A與點O在BC的兩側時,如圖1,OA=AD+OD=4+1=5;
當點A與點O在BC的同側時,如圖2,OA=AD﹣OD=4﹣1=3,
故OA的長為3或5.
故答案為:3或5.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】閱讀:小明用下面的方法求![]() 的解.
的解.
解法 1:令![]() ,則x=t2,原方程化為t -3t2=0,解方程t -3t2=0,得t1=0,t2=
,則x=t2,原方程化為t -3t2=0,解方程t -3t2=0,得t1=0,t2=![]() ,
,
所以![]() 或
或![]() ,將方程
,將方程![]() 或
或![]() 兩邊平方,得x=0或
兩邊平方,得x=0或![]() .
.
經檢驗:x=0或![]() 都是原方程的解,所以原方程的解為x=0或
都是原方程的解,所以原方程的解為x=0或![]() .
.
解法 2:移項,得 ![]() ,方程兩邊同時平方,得x=9x2,解方程x=9x2,得x=0或
,方程兩邊同時平方,得x=9x2,解方程x=9x2,得x=0或![]() .
.
經檢驗:x=0或![]() 都是原方程的解,所以原方程的解為x=0或
都是原方程的解,所以原方程的解為x=0或![]() .
.
(1)定義![]() ,根據定義寫出符合條件
,根據定義寫出符合條件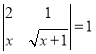 的方程;
的方程;
(2)求出(1)中寫出的方程的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,拋物線與![]() 軸交點坐標為
軸交點坐標為![]() ,
,![]()
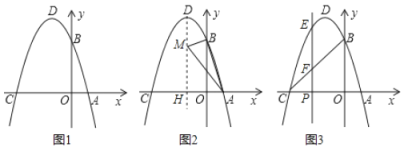
(1)如圖1,已知頂點坐標![]() 為
為![]() 或
或![]() 點
點![]() ,選擇適當方法求拋物線的解析式;
,選擇適當方法求拋物線的解析式;
(2)如圖2,在(1)的條件下,在拋物線的對稱軸![]() 上求作一點
上求作一點![]() ,使
,使![]() 的周長最小,并求出點
的周長最小,并求出點![]() 的坐標;
的坐標;
(3)如圖3,在(1)的條件下,將圖2中的對稱軸向左移動,交![]() 軸于點
軸于點![]() ,與拋物線,線段
,與拋物線,線段![]() 的交點分別為點
的交點分別為點![]() 、
、![]() ,用含
,用含![]() 的代數式表示線段
的代數式表示線段![]() 的長度,并求出當
的長度,并求出當![]() 為何值時,線段
為何值時,線段![]() 最長.
最長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 在直線
在直線![]() 上運動,把點
上運動,把點![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() ,點
,點![]() 的對應點為點
的對應點為點![]() ,我們發現點
,我們發現點![]() 隨點
隨點![]() 變化而變化.若點
變化而變化.若點![]() 在運動變化過程中始終在拋物線
在運動變化過程中始終在拋物線![]() 的上方,設點
的上方,設點![]() 的橫坐標為
的橫坐標為![]() ,則
,則![]() 的取值范圍是______.
的取值范圍是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與⊙O相切于點D,過圓心O作EF∥
與⊙O相切于點D,過圓心O作EF∥![]() 交⊙O于E、F兩點,點A是⊙O上一點,連接AE,AF,并分別延長交直線
交⊙O于E、F兩點,點A是⊙O上一點,連接AE,AF,并分別延長交直線![]() 于B、C兩點;
于B、C兩點;
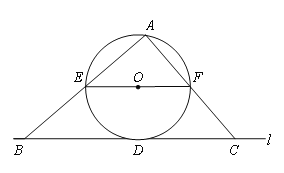
(1)求證:∠ABC+∠ACB=90°;
(2)若⊙O的半徑![]() ,BD=12,求tan∠ACB的值.
,BD=12,求tan∠ACB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年,號稱“千湖之省”的湖北正遭受大旱,為提高學生環境意識,節約用水,某校數學教師編制了一道應用題:為了保護水資源,某市制定一套節水的管理措施,其中對居民生活用水收費作如下規定:
月用水量(噸) | 單價(元/噸) |
不大于10噸部分 | 1.5 |
大于10噸不大于m噸部分(20≤m≤50) | 2 |
大于m噸部分 | 3 |
(1)若某用戶六月份用水量為18噸,求其應繳納的水費;
(2)記該用戶六月份用水量為![]() 噸,繳納水費為
噸,繳納水費為![]() 元,試列出
元,試列出![]() 與
與![]() 的函數式;
的函數式;
(3)若該用戶六月份用水量為40噸,繳納水費![]() 元的取值范圍為
元的取值范圍為![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
各位同學,請你也認真做一做,相信聰明的你一定會順利完成.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 過點
過點![]() ,頂點為M,與x軸交于AB兩點,D為AB的中點,
,頂點為M,與x軸交于AB兩點,D為AB的中點,![]() 軸,交拋物線于點E,下列結論中正確的是( )
軸,交拋物線于點E,下列結論中正確的是( )
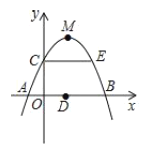
A.拋物線的對稱軸是直線x=-3B.![]()
C.![]() D.四邊形ADEC是菱形
D.四邊形ADEC是菱形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊用周長為![]() 米的籬笆圍成.已知墻長
米的籬笆圍成.已知墻長![]() 米(如圖所示),設這個苗圃園垂直于墻的一邊長為
米(如圖所示),設這個苗圃園垂直于墻的一邊長為![]() 米.
米.
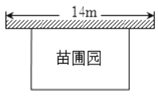
(1)若苗圃園的面積為![]() 平方米,求
平方米,求![]() 的值;
的值;
(2)若平行于墻的一邊長不小于![]() 米,這個苗圃園的面積
米,這個苗圃園的面積![]() 有最大值嗎?如果有,求出最大值;如果沒有,請說明理由.
有最大值嗎?如果有,求出最大值;如果沒有,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com