
【題目】珠海市水務局對某小區居民生活用水情況進行了調査.隨機抽取部分家庭進行統計,繪制成如下尚未完成的頻數分布表和頻率分布直方圖.請根據圖表,解答下列問題:
月均用水量(單位:噸 | 頻數 | 頻率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合計 | d | 1.00 |

(1)b= ,c= ,并補全頻數分布直方圖;
(2)為鼓勵節約用水用水,現要確定一個用水量標準P(單位:噸),超過這個標準的部分按1.5倍的價格收費,若要使60%的家庭水費支出不受影響,則這個用水量標準P= 噸;
(3)根據該樣本,請估計該小區400戶家庭中月均用水量不少于5噸的家庭約有多少戶?
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】【探究函數y=x+![]() 的圖象與性質】
的圖象與性質】
(1)函數y=x+![]() 的自變量x的取值范圍是________;
的自變量x的取值范圍是________;
(2)下列四個函數圖象中,函數y=x+![]() 的圖象大致是________;
的圖象大致是________;

(3)對于函數y=x+![]() ,求當x>0時,y的取值范圍.請將下列的求解過程補充完整.
,求當x>0時,y的取值范圍.請將下列的求解過程補充完整.
解:∵x>0,∴y=x+![]() =(
=(![]() )2+
)2+![]() =
=![]() +________.
+________.
∵![]() ≥0,∴y≥________.
≥0,∴y≥________.
【拓展運用】
(4)若函數y=![]() ,求y的取值范圍.
,求y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點M,與BC相交于點N.連接BM,DN.
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在![]() 中,已知AB=AC,垂足為點D,點F在AD的延長線上,且CE∥BF,試說明DE=DF的理由.
中,已知AB=AC,垂足為點D,點F在AD的延長線上,且CE∥BF,試說明DE=DF的理由.

解:因為AB=AC,AD⊥BC(已知)
所以BD=
因為CE∥BF(已知)
所以![]() =
=
在![]() 中,
中,
![]() 中
中
=
=
所以![]() ( )
( )
所以DE=DF( )
查看答案和解析>>
科目:初中數學 來源: 題型:
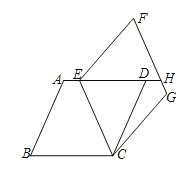
【題目】如圖,完全相同的兩個菱形ABCD和ECGF的頂點C重合,∠B=∠F,點E恰好在邊AD上,延長ED交FG于點H.
(1)求證:∠B=∠ECB;
(2)連接BE、CH.
①試判斷四邊形BEHC的形狀,并說理理由;
②求證:CH平分∠DCG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】撫順某中學為了解八年級學生的體能狀況,從八年級學生中隨機抽取部分學生進行體能測試,測試結果分為A,B,C,D四個等級.請根據兩幅統計圖中的信息回答下列問題:
(1)本次抽樣調查共抽取了多少名學生?
(2)求測試結果為C等級的學生數,并補全條形圖;
(3)若該中學八年級共有700名學生,請你估計該中學八年級學生中體能測試結果為D等級的學生有多少名?
(4)若從體能為A等級的2名男生2名女生中隨機的抽取2名學生,做為該校培養運動員的重點對象,請用列表法或畫樹狀圖的方法求所抽取的兩人恰好都是男生的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知平行四邊形ABCO,以點O為原點,OC所在的直線為x軸,建立直角坐標系,AB交y軸于點D,AD=4,OC=10,∠A=60°,線段EF垂直平分OD,點P為線段EF上的動點,PM⊥x軸于點M點,點E與E'關于x軸對稱,連接BP、E'M,則BP+PM+ME'的長度的最小值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場計劃撥款9萬元從廠家購進50臺電視機,已知該廠生產三種不同型號的電視機,出廠價分別為甲種每臺1500元, 乙種每臺2100元, 丙種每臺2500元, 若商場同時購進其中兩種不同型號的電視機共50臺,用去9萬元.請你通過計算,說明商場有哪些進貨方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com