
【題目】甲、乙兩輛汽車分別從A、B兩地同時出發,沿同一條公路相向而行,乙車出發2h后休息,與甲車相遇后,繼續行駛.設甲、乙兩車與B地的路程分別為y甲(km),y乙(km),甲車行駛的時間為x(h),y甲、y乙與x之間的函數圖象如圖所示,結合圖象解答下列問題:
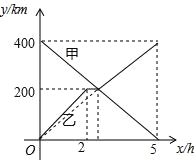
(1)乙車休息了 h.
(2)求乙車與甲車相遇后y乙關于x的函數表達式,并寫出自變量x的取值范圍.
(3)當兩車相距40km時,求x的值.
【答案】(1)0.5;(2)y乙=80x;(3)x=2或x=![]() .
.
【解析】
試題分析:(1)先把y=200代入甲的函數關系式中,可得x的值,再由圖象可知乙車休息的時間;
(2)根據待定系數法,可得休息后,乙車與甲車相遇后y乙關于x的函數表達式;
(3)分類討論,0≤x<2.5,y甲減y乙等于40千米,2.5≤x≤5時,y乙減y甲等于40千米即可.
試題解析:(1)設甲車與B地的距離y(km)與行駛時間x(h)之間的函數關系式為y=kx+b,
可得:![]() ,
,
解得:![]() .
.
所以函數解析式為:y=-80x+400;
把y=200代入y=-80x+400中,可得:200=-80x+400,
解得:x=2.5,
所以乙車休息的時間為:2.5-2=0.5小時;
(2)設乙車與甲車相遇后y乙關于x的函數表達式為:y乙=k1x+b1,
y乙=k1x+b1圖象過點(2.5,200),(5,400),
得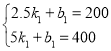 ,
,
解得 ,
,
乙車與甲車相遇后y乙與x的函數解析式y乙=80x;
(3)設乙車與甲車相遇前y乙與x的函數解析式y乙=kx,圖象過點(2,200),
解得k=100,
∴乙車與甲車相遇前y乙與x的函數解析式y乙=100x,
0≤x<2.5,y甲減y乙等于40千米,
即400-80x-100x=40,解得 x=2;
2.5≤x≤5時,y乙減y甲等于40千米,
即2.5≤x≤5時,80x-(-80x+400)=40,解得x=![]() ,
,
綜上所述:x=2或x=![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法正確的有( )
①所有的有理數都能用數軸上的點表示;
②符號不同的兩個數互為相反數;
③有理數分為正數和負數;
④兩數相減,差一定小于被減數;
⑤兩數相加,和一定大于任何一個加數.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋轉得到的.
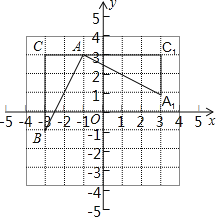
(1)請寫出旋轉中心的坐標是 ,旋轉角是 度;
(2)以(1)中的旋轉中心為中心,分別畫出△A1AC1順時針旋轉90°、180°的三角形;
(3)設Rt△ABC兩直角邊BC=a、AC=b、斜邊AB=c,利用變換前后所形成的圖案證明勾股定理.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知不等邊三角形的兩邊長分別是2cm和9cm,如果第三邊的長為整數,那么第三邊的長為( )
A.8cm
B.10cm
C.8cm或10cm
D.8cm或9cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將△AOB繞原點O順時針旋轉180°后得到△A1OB1,若點B的坐標為(2,1),則點B的對應點B1的坐標為( )
A. (﹣2,﹣1) B. (2,﹣1) C. (﹣2,1) D. (1,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文明,源遠流長:中華漢字,寓意深廣,為了傳承優秀傳統文化,某校團委組織了一次全校3000名學生參加的“漢字聽寫”大賽,賽后發現所有參賽學生的成績均不低于50分.為了更好地了解本次大賽的成績分布情況,隨機抽取了其中200名學生的成績(成績x取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
成績x/分 | 頻數 | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
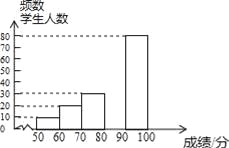
請根據所給信息,解答下列問題:
(1)a=______,b=______;
(2)請補全頻數分布直方圖;
(3)這次比賽成績的中位數會落在_____________分數段;
(4)若成績在90分以上(包括90分)的為“優”等,則該校參加這次比賽的3000名學生中成績“優”等約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABE和△ACD是△ABC分別以AB、AC為對稱軸翻折180°形成的,若∠1︰∠2︰∠3=28︰5︰3,則∠α度數為______________;

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com