
【題目】如圖,以BC為底邊的等腰△ABC,點D,E,G分別在BC,AB,AC上,且EG∥BC,DE∥AC,延長GE至點F,使得BE=BF.
(1)求證:四邊形BDEF為平行四邊形;
(2)當∠C=45°,BD=2時,求D,F兩點間的距離.

【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)由等腰三角形的性質得出∠ABC=∠C,證出∠AEG=∠ABC=∠C,四邊形CDEG是平行四邊形,得出∠DEG=∠C,證出∠F=∠DEG,得出BF∥DE,即可得出結論;
(2)證出△BDE、△BEF是等腰直角三角形,由勾股定理得出BF的值,作FM⊥BD于M,連接DF,則△BFM是等腰直角三角形,由勾股定理得出FM的值,進而得出DM=3,在Rt△DFM中,由勾股定理求出DF即可.
試題解析:(1)證明:∵△ABC是等腰三角形,∴∠ABC=∠C,∵EG∥BC,DE∥AC,∴∠AEG=∠ABC=∠C,四邊形CDEG是平行四邊形,∴∠DEG=∠C,∵BE=BF,∴∠BFE=∠BEF=∠AEG=∠ABC,∴∠F=∠DEG,∴BF∥DE,∴四邊形BDEF為平行四邊形;
(2)解:∵∠C=45°,∴∠ABC=∠BFE=∠BEF=45°,∴△BDE、△BEF是等腰直角三角形,∴BF=BE=![]() BD=
BD=![]() ,作FM⊥BD于M,連接DF,如圖所示:
,作FM⊥BD于M,連接DF,如圖所示:
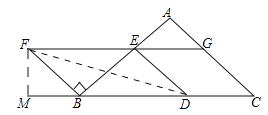
則△BFM是等腰直角三角形,∴FM=BM=![]() BF=1,∴DM=3,在Rt△DFM中,由勾股定理得:DF=
BF=1,∴DM=3,在Rt△DFM中,由勾股定理得:DF=![]() =
=![]() ,即D,F兩點間的距離為
,即D,F兩點間的距離為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】有兩個可以自由轉動的均勻轉盤A、B,都被分成了3等份,并在每份內均標有數字,如圖所示,規則如下:
①分別轉動轉盤A、B.
②兩個轉盤停止后,將兩個指針所指份內的數字相乘(若指針停在等分線上,那么重轉一次,直到指針指向某一份為止).
(1)用列表法(或樹狀圖)分別求出數字之積為3的倍數和為5的倍數的概率;
(2)小亮和小蕓想用這兩個轉盤做游戲,他們規定:數字之積為3的倍數時,小亮得2分;數字之積為5的倍數時,小蕓得3分.這個游戲對雙方公平嗎?請說明理由;認為不公平的,試修改得分規定,使游戲雙方公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰△ABC中,AB=AC,BD,CE分別是邊AC,AB上的中線,BD與CE相交于點O,點M,N分別為線段BO和CO的中點.求證:四邊形EDNM是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校學生的身高情況,隨機抽取該校男生、女生進行抽樣調查.已知抽取的樣本中,男生、女生的人數相同,利用所得數據繪制如下統計圖表:(A組:x<155; B組:155≤x<160; C組:160≤x<165; D組165≤x<170;E組:x≥170) 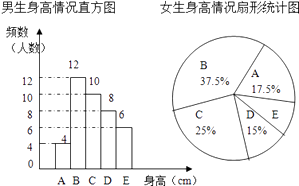
根據圖表提供的信息,回答下列問題:
(1)樣本中,男生的身高眾數在組,中位數在組.
(2)樣本中,女生的身高在E組的人數有人.
(3)已知該校共有男生400人,女生380人,請估計身高在160≤x<170之間的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲騎自行車從A地出發,以每小時15km的速度駛向B地,經半小時后乙騎自行車從B地出發,以每小時20km的速度駛向A地,兩人相遇時,乙已超過AB兩地的中點5km,求A、B兩地的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,點E是AD上的一點,有AE=4,BE的垂直平分線交BC的延長線于點F,連結EF交CD于點G.若G是CD的中點,則BC的長是 . 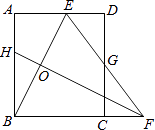
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校計劃從某苗木基地購進A、B兩咱樹苗共200棵綠化校園。已知購買了3棵A種樹苗和5棵B種樹苗共需700元;購買2棵A種樹苗和1棵B種樹苗共需280元.
(1)每棵A種樹苗、B種樹苗各需多少元?
(2)學校除支付購買樹苗的費用外,平均每棵樹苗還需支付運輸及種植費用20元。設學校購買B種樹苗x棵,購買兩種樹苗及運輸、種植所需的總費用為y元,求y與x的函數關系;
(3)在(2)的條件下,若學校用于綠化的總費用在22400元限額內,且購買A種樹苗的數量不少于B種樹苗的數量,請給出一種費用最省的方案,并求出該方案所需的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個有45°角的三角板的直角頂點放在一張寬為3cm的紙帶邊沿上,另一個頂
點在紙帶的另一邊沿上,測得三角板的一邊與紙帶的一邊所在的直線成30°角,如圖(3),
則三角板的最大邊的長為( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學每天中午總是在規定時間打開學校大門,七年級同學小明每天中午同一時間從家騎自行車到學校,星期一中午他以每小時15千米的速度到校,結果在校門口等了6分鐘才開門,星期二中午他以每小時9千米的速度到校,結果校門已開了6分鐘,星期三中午小明想準時到達學校門口,那么小明騎自行車的速度應該為每小時多少千米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com