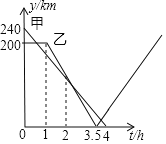
【題目】在一條筆直的公路上有A、B、C三地，C地位于A、B兩地之間．甲車從A地沿這條公路勻速駛向C地，乙車從B地沿這條公路勻速駛向A地，在甲、乙行駛過程中，甲、乙兩車各自與C地的距離y（km）與甲車行駛時間t（h）之間的函數關系如圖所示．則當乙車到達A地時，甲車已在C地休息了_____小時．
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=x+4的圖象與反比例函數y=
（k為常數且k≠0）的圖象交于A（﹣1，a），B兩點，與x軸交于點C．
（1）求此反比例函數的表達式；
（2）若點P在x軸上，且S△ACP=
S△BOC，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
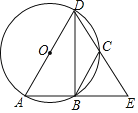
【題目】如圖：AD是⊙O的直徑，AD＝12，點BC在⊙O上，AB、DC的延長線交于點E，且CB＝CE，∠BCE＝70°，則以下判斷中不正確的是（ ）
A.∠ADE＝∠EB.劣弧AB的長為
π
C.點C為弧BD的中點D.BD平分∠ADE
查看答案和解析>>
科目：初中數學 來源： 題型：
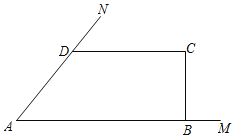
【題目】某市政府為了扶貧，鼓勵當地農民養殖小龍蝦，如圖：張叔叔順著圩梗AN、AM（AN＝3
m，AM＝10m，∠MAN＝45°），用8m長的漁網搭建了一個養殖水域（即四邊形ABCD），圩梗邊不需要漁網，AB∥CD，∠C＝90°．設BC＝xm，四邊形ABCD面積為S（m2）．
（1）求出S關于x的函數表達式及x的取值范圍；
（2）x為何值時，圍成的養殖水域面積最大？最大面積是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
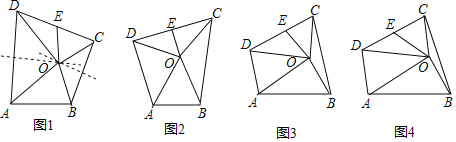
【題目】如圖1，四邊形ABCD，邊AD、BC的垂直平分線相交于點O．連接OA、OB、OC、OD．OE是邊CD的中線，且∠AOB+∠COD＝180°
（1）如圖2，當△ABO是等邊三角形時，求證：OE＝
AB；
（2）如圖3，當△ABO是直角三角形時，且∠AOB＝90°，求證：OE＝AB；
（3）如圖4，當△ABO是任意三角形時，設∠OAD＝α，∠OBC＝β，
①試探究α、β之間存在的數量關系？
②結論“OE＝AB”還成立嗎？若成立，請你證明；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校初三（1）班50名學生需要參加體育“五選一”自選項目測試，班上學生所報自選項目的情況統計表如下：
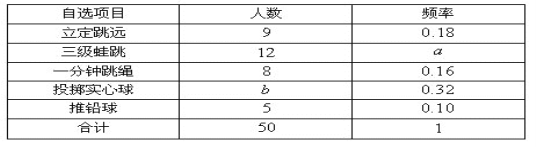
(1)求a，b的值；
(2)若將各自選項目的人數所占比例繪制成扇形統計圖，求“一分鐘跳繩”對應扇形的圓心角的度數；
(3)在選報“推鉛球”的學生中，有3名男生，2名女生．為了了解學生的訓練效果，從這5名學生中隨機抽取兩名學生進行推鉛球測試，求所抽取的兩名學生中至多有一名女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校擬派一名跳高運動員參加校際比賽，對甲、乙兩名同學進行了8次跳高選拔比賽，他們的原始成績（單位：cm）如下表：
學生/成績/次數 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 |
甲 | 169 | 165 | 168 | 169 | 172 | 173 | 169 | 167 |
乙 | 161 | 174 | 172 | 162 | 163 | 172 | 172 | 176 |
兩名同學的8次跳高成績數據分析如下表：
學生/成績/名稱 | 平均數（單位：cm） | 中位數（單位：cm） | 眾數（單位：cm） | 方差（單位：cm2） |
甲 | a | b | c | 5.75 |
乙 | 169 | 172 | 172 | 31.25 |
根據圖表信息回答下列問題：
（1）a＝ ，b＝ ，c＝ ；
（2）這兩名同學中， 的成績更為穩定；（填甲或乙）
（3）若預測跳高165就可能獲得冠軍，該校為了獲取跳高比賽冠軍，你認為應該選擇 同學參賽，理由是： ；
（4）若預測跳高170方可奪得冠軍，該校為了獲取跳高比賽冠軍，你認為應該選擇 同學參賽，班由是： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC為等邊三角形，點D為直線BC上的一動點（點D不與B、C重合），以AD為邊作菱形ADEF（A、D、E、F按逆時針排列），使∠DAF=60°，連接CF．
（1）如圖1，當點D在邊BC上時，求證：①BD=CF；②AC=CF+CD；
（2）如圖2，當點D在邊BC的延長線上且其他條件不變時，結論AC=CF+CD是否成立？若不成立，請寫出AC、CF、CD之間存在的數量關系，并說明理由；
（3）如圖3，當點D在邊BC的延長線上且其他條件不變時，補全圖形，并直接寫出AC、CF、CD之間存在的數量關系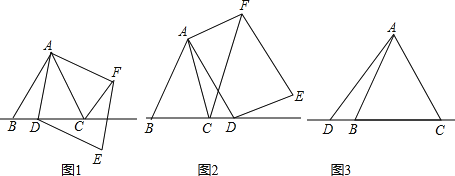
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
