【答案】
分析:先全部通分,得到分母=40!,分子=40!+

+
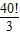
+…+

,再將分子與分母中5的倍數約掉,即可發現m不會是5的倍數.
解答:證明:通分得,

=

(40!=1×2×3×…×40).
觀察發現:分母包括9個5的乘積(5,10,15,20,25,30,35,40),即分母含有因數5
9.如果m是5的倍數,那么分子至少包括10個5的乘積.
現在看分子:分子是40個數的和,其中每一個數都是1×2×3×…×40除以一個1到40的數,這40個數中有32個數是5
9的倍數(就是除以的那個數不是5的倍數),7個數是5
8的倍數(除以的那個數是5的倍數但不是25),1個數是5
7的倍數(除以的數是25),所以,分子可以寫成5
7(5
2A+5B+C),由于(5
2A+5B)是5的倍數,而C不是5的倍數,所以(5
2A+5B+C)不是5的倍數,即分子僅包含5
7,而分母包含5
9,所以約分后的分子(5
2A+5B+C)不是5的倍數.
即將和

寫成最簡分數
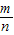
時,m不會是5的倍數.
點評:本題考查了質因數分解,屬于競賽題型,有一定難度,找出通分后分子與分母的公因數5
7是解題的關鍵.

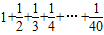 寫成最簡分數
寫成最簡分數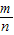 時,m不會是5的倍數.
時,m不會是5的倍數. +
+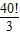 +…+
+…+ ,再將分子與分母中5的倍數約掉,即可發現m不會是5的倍數.
,再將分子與分母中5的倍數約掉,即可發現m不會是5的倍數. =
= (40!=1×2×3×…×40).
(40!=1×2×3×…×40). 寫成最簡分數
寫成最簡分數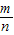 時,m不會是5的倍數.
時,m不會是5的倍數.

 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案