
 取了該年級50名學生進行了調查,根據調查所得的數據制成如圖的頻數分布直方圖.
取了該年級50名學生進行了調查,根據調查所得的數據制成如圖的頻數分布直方圖.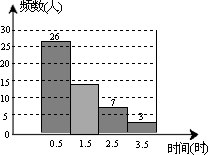 解:(1)根據直方圖中各個小組的頻數之和等于總數,可得第二組的頻數為50-26-7-3=14;據此可補全直方圖;
解:(1)根據直方圖中各個小組的頻數之和等于總數,可得第二組的頻數為50-26-7-3=14;據此可補全直方圖;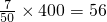 人;
人; ,進行計算可得答案;
,進行計算可得答案;

科目:初中數學 來源: 題型:
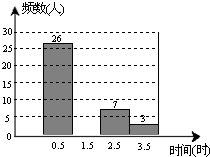 取了該年級50名學生進行了調查,根據調查所得的數據制成如圖的頻數分布直方圖.
取了該年級50名學生進行了調查,根據調查所得的數據制成如圖的頻數分布直方圖.查看答案和解析>>
科目:初中數學 來源:期末題 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com