解方程:
(1)(x-1)2-25=0 (2)2(x+1)2=x2-1
(3)2x2+6x+1=0(用配方法解) (4)(x+5)2-2(x+5)-8=0.
【答案】
分析:(1)利用直接開平方法解方程;
(2)利用因式分解法解方程;
(3)配方法解方程;
(4)因式分解法解方程.
解答:解:(1)由原方程,移項,得
(x-1)
2=25,
開平方,得
x-1=±5,
∴x=1±5,
∴x
1=6 x
2=-4;
(2)由原方程,得
2x
2+4x+2=x
2-1,即x
2+4x+3=0,
∴(x+1)(x+3)=0,
∴x+1=0或x+3=0,
解得,x
1=-1,x
2=-3;
(3)化二次項系數(shù)為1,得
x
2+3x+

=0,
移項,得
x
2+3x=-

,
等式的兩邊同時加上一次項系數(shù)一半的平方,得
x
2+3x+

=

-

,
∴(x+

)
2=

,
∴x=-
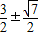
,
解得,x
1=
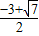
,x
2=
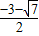
;
(4)由原方程,得
(x+5+2)(x+5-4)=0,即(x+7)(x+1)=0,
∴x+7=0,或x+1=0,
解得,x
1=-1,x
2=-7.
點評:本題考查了配方法、因式分解法、直接開平法解方程.對于解方程的方法的選擇,應(yīng)該根據(jù)方程的特點選擇不同的方法.

 =0,
=0, ,
, =
= -
- ,
, )2=
)2= ,
,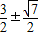 ,
,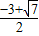 ,x2=
,x2=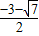 ;
;

 閱讀快車系列答案
閱讀快車系列答案