
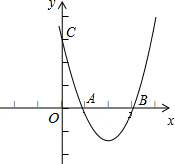
 已知:如圖,拋物線y=ax2+bx+c與x軸相交于兩點A(1,0),B(3,0)與y軸相交于點C(0,3),
已知:如圖,拋物線y=ax2+bx+c與x軸相交于兩點A(1,0),B(3,0)與y軸相交于點C(0,3), ×(3-1)×3=3;
×(3-1)×3=3;

 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案科目:初中數學 來源: 題型:
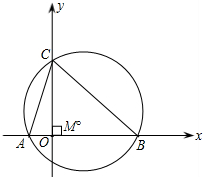 與y軸交點C的縱坐標為3,△ABC的外接圓的圓心為點M.
與y軸交點C的縱坐標為3,△ABC的外接圓的圓心為點M.查看答案和解析>>
科目:初中數學 來源: 題型:
 此拋物線上,矩形面積為12,
此拋物線上,矩形面積為12,查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•寧化縣質檢)已知:如圖,拋物線y=ax2+bx+c與x軸交于點A(1-
(2013•寧化縣質檢)已知:如圖,拋物線y=ax2+bx+c與x軸交于點A(1-| 3 |
| ||
| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知,如圖,拋物線y=ax2-2ax+c(a≠0)與y軸交于點C(0,4),與x軸交于點A,B,點A的坐標為(4,0).
已知,如圖,拋物線y=ax2-2ax+c(a≠0)與y軸交于點C(0,4),與x軸交于點A,B,點A的坐標為(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:
 已知,如圖,拋物線y=x2+px+q與x軸相交于A、B兩點,與y軸交于點C,且OA≠OB,OA=OC,設拋物線的頂點為點P,直線PC與x軸的交點D恰好與點A關于y軸對稱.
已知,如圖,拋物線y=x2+px+q與x軸相交于A、B兩點,與y軸交于點C,且OA≠OB,OA=OC,設拋物線的頂點為點P,直線PC與x軸的交點D恰好與點A關于y軸對稱.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com