
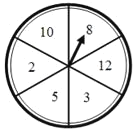
【題目】小亮、小穎的手上都有兩根長度分別為5、8的木棒,小亮與小穎都想通過轉動轉盤游戲來獲取第三根木棒,如圖,一個均勻的轉盤被平均分成6等份,分別標有木棒的長度2,3,5,8,10,12這6個數字.小亮與小穎各轉動轉盤一次,停止后,指針指向的數字即為轉出的第三根木棒的長度.若三根木棒能組成三角形則小亮獲勝,三根木棒能組成等腰三角形則小穎獲勝.
(1)小亮獲勝的概率是 ;
(2)小穎獲勝的概率是 ;
(3)請你用這個轉盤設計一個游戲,使得對小亮與小穎均是公平的;
(4)小穎發現,她連續轉動轉盤10次,都沒轉到5和8,能不能就說小穎獲勝的可能性為0?為什么?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析;(4)不能,理由見解析.
;(3)見解析;(4)不能,理由見解析.
【解析】
(1)設構成三角形的第三根木棒的長度為x,由三角形三邊關系可知3<x<13,在所給的6個數字中,有4個數字滿足條件,則可求小亮獲勝的概率.(2)在所給的6個數字中,有2個數字滿足條件,則可求小穎獲勝的概率.(3)答案不唯一,只要使得小亮與小穎獲勝的概率相同即可.(4)不能,只能說明可能性小,但并不一定為0.
解:
(1)設構成三角形的第三根木棒的長度為x,
則8﹣5<x<5+8,即3<x<13,
∵在2,3,5,8,10,12這6個數字中,能構成三角形的有5、8、10、12這四個,
∴小亮獲勝的概率是![]() =
=![]() ,
,
故答案為:![]() .
.
(2)∵在2,3,5,8,10,12這6個數字中,能構成等腰三角形的有5,8這兩個,
∴小穎獲勝的概率是![]() =
=![]() .
.
(3)小亮轉動轉盤一次,停止后指針指向的數字即為轉出的第三根木棒的長度.若三根木棒能組成三角形則小亮獲勝;小穎轉動轉盤一次,停止后指針指向的數字為偶數,則小穎獲勝.
(4)不能,她連續轉動轉盤10次,都沒轉到5和8,只是說明可能性小,但并不一定為0.


科目:初中數學 來源: 題型:
【題目】如圖,將△ABC沿射線BC方向平移3 cm得到△DEF.若△ABC的周長為14 cm,則四邊形ABFD的周長為( )

A. 20 cmB. 17 cm
C. 14 cmD. 23 cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作體驗:如圖,在矩形ABCD中,點E、F分別在邊AD、BC上,將矩形ABCD沿直線EF折疊,使點D恰好與點B重合,點C落在點C'處.點P為直線EF上一動點(不與E、F重合),過點P分別作直線BE、BF的垂線,垂足分別為點M和N,以PM、PN為鄰邊構造平行四邊形PMQN.
(1)如圖1,求證:BE=BF;
(2)特例感知:如圖2,若DE=5,CF=3,當點P在線段EF上運動時,求平行四邊形PMQN的周長;
(3)類比探究:如圖3,當點P在線段EF的延長線上運動時,若DE=a,CF=b.請直接用含a、b的式子表示QM與QN之間的數量關系.(不要求寫證明過程)

查看答案和解析>>
科目:初中數學 來源: 題型:
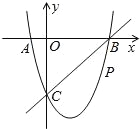
【題目】如圖,在平面直角坐標系中,二次函數y=x2+bx+c的圖象與x軸交于A、B兩點,A點在原點左側,B點的坐標為(4,0),與y軸交于C(0,﹣4)點,點P是直線BC下方的拋物線上一動點.
(1)求這個二次函數的表達式.
(2)連接PO、PC,并把△POC沿CO翻折,得到四邊形POP′C,那么是否存在點P,使四邊形POP′C為菱形?若存在,請求出此時點P的坐標;若不存在,請說明理由.
(3)當點P運動到什么位置時,四邊形ABPC的面積最大?求出此時P點的坐標和四邊形ABPC的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是射線BM上的一個動點(點P不與點B重合),∠AOB= 30°,∠ABM=60°.當∠OAP=______時,以點A、O、B中的任意兩點和點P為頂點的三角形是等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+bx+c(a≠0)的頂點為C(1,4),交x軸于A、B兩點,交y軸于點 D,其中點B的坐標為(3,0).
(1)求拋物線的解析式;
(2)如圖2,過點A的直線與拋物線交于點E,交y軸于點F,其中點E的橫坐標為2,若直線PQ為拋物線的對稱軸,點G為直線PQ上的一動點,則x軸上是否存在一點H,使D、G、H、F四點所圍成的四邊形周長最小;若存在,求出這個最小值及點G、H的坐標;若不存在,請說明理由.
(3)如圖3,在拋物線上是否存在一點T,過點T作x軸的垂線,垂足為點M,過點M作MN∥BD,交線段AD于點N,連接MD,使△DNM∽△BMD。若存在,求出點T的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學興趣小組活動中,李燕和劉凱兩位同學設計了如圖所示的兩個轉盤做游戲(每個轉盤被分成面積相等的幾個扇形,并在每個扇形區域內標上數字).游戲規則如下:兩人分別同時轉動甲、乙轉盤,轉盤停止后,若指針所指區域內兩數和小于12,則李燕獲勝;若指針所指區域內兩數和等于12,則為平局;若指針所指區域內兩數和大于12,則劉凱獲勝(若指針停在等分線上,重轉一次,直到指針指向某一份內為止).
(1)請用列表或畫樹狀圖的方法表示出上述游戲中兩數和的所有可能的結果;
(2)分別求出李燕和劉凱獲勝的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過類比聯想、引申拓展研究典型題目,可達到解一題知一類的目的.下面是一個案例.
原題:如圖①,點![]() 分別在正方形
分別在正方形![]() 的邊
的邊![]() 上,
上, ![]() ,連接
,連接![]() ,則
,則![]() ,試說明理由.
,試說明理由.

(1)思路梳理
因為![]() ,所以把
,所以把![]() 繞點
繞點![]() 逆時針旋轉90°至
逆時針旋轉90°至![]() ,可使
,可使![]() 與
與![]() 重合.因為
重合.因為![]() ,所以
,所以![]() ,點
,點![]() 共線.
共線.
根據 ,易證![]() ,得
,得![]() .請證明.
.請證明.
(2)類比引申
如圖②,四邊形![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 分別在邊
分別在邊![]() 上,
上, ![]() .若
.若![]() 都不是直角,則當
都不是直角,則當![]() 與
與![]() 滿足等量關系時,
滿足等量關系時, ![]() 仍然成立,請證明.
仍然成立,請證明.
(3)聯想拓展
如圖③,在![]() 中,
中, ![]() ,點
,點![]() 均在邊
均在邊![]() 上,且
上,且![]() .猜想
.猜想![]() 應滿足的等量關系,并寫出證明過程.
應滿足的等量關系,并寫出證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c交x軸于(﹣1,0)、(3,0)兩點,以下四個結論正確的是(用序號表示)______________.
(1)圖象的對稱軸是直線 x=1
(2)當x>1時,y隨x的增大而減小
(3)一元二次方程ax2+bx+c=0的兩個根是﹣1和3
(4)當﹣1<x<3時,y<0.
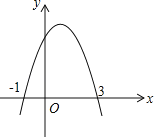
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com