
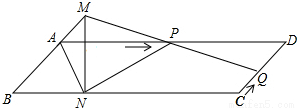
 已知:如圖,?ABCD中,AD=3cm,CD=1cm,∠B=45°,點P從點A出發(fā),沿AD方向勻速運動,速度為3cm/s;點Q從點C出發(fā),沿CD方向勻速運動,速度為1cm/s,連接并延長QP交BA的延長線于點M,過M作MN⊥BC,垂足是N,設(shè)運動時間為t(s)(0<t<1)
已知:如圖,?ABCD中,AD=3cm,CD=1cm,∠B=45°,點P從點A出發(fā),沿AD方向勻速運動,速度為3cm/s;點Q從點C出發(fā),沿CD方向勻速運動,速度為1cm/s,連接并延長QP交BA的延長線于點M,過M作MN⊥BC,垂足是N,設(shè)運動時間為t(s)(0<t<1)分析 (1)首先根據(jù)BM∥CD,可得$\frac{AM}{DQ}=\frac{AP}{DP}$,據(jù)此求出AM的值是多少;然后判斷出△BMN是等腰直角三角形,即可求出MN的值是多少.
(2)首先判斷出MN⊥AD,然后根據(jù)四邊形ANPM的面積為$\frac{9\sqrt{2}}{16}$cm2,可得$\frac{1}{2}$×$\frac{\sqrt{2}}{2}(t+1)$×3t=$\frac{9\sqrt{2}}{16}$,據(jù)此求出t的值是多少即可.
(3)首先判斷出AM=QD,然后根據(jù)AM∥QD,推得四邊形MAQD是平行四邊形即可.
(4)存在某一時刻t,使AO:OC=$\sqrt{2}$:1.根據(jù)AD∥BC,可得$\frac{AP}{CN}=\frac{AO}{OC}$,所以$\frac{3t}{3-\frac{\sqrt{2}}{2}(t+1)}=\sqrt{2}$,據(jù)此求出t的值是多少即可.
解答 解:(1)∵BM∥CD,
∴$\frac{AM}{DQ}=\frac{AP}{DP}$,
∴$\frac{AM}{1-t}=\frac{3t}{3-3t}$,
解得AM=t.
∵MN⊥BC,
∴∠MNB=90°,
又∵∠B=45°,
∴MN=$\frac{\sqrt{2}}{2}$BM=$\frac{\sqrt{2}}{2}(t+1)$.
(2)∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∵MN⊥BC,
∴MN⊥AD,
∵四邊形ANPM的面積為$\frac{9\sqrt{2}}{16}$cm2,
∴$\frac{1}{2}$×$\frac{\sqrt{2}}{2}(t+1)$×3t=$\frac{9\sqrt{2}}{16}$,
整理,可得4t2+4t-3=0,
解得t=$\frac{1}{2}$或t=-$\frac{3}{2}$(舍去),
∴四邊形ANPM的面積為$\frac{9\sqrt{2}}{16}$cm2,t的值是$\frac{1}{2}$.
(3)如圖1,連接MD、AQ,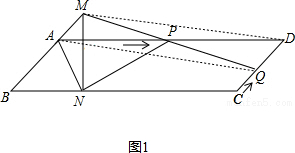 ,
,
由(2),可得t=$\frac{1}{2}$,
∴AM=$\frac{1}{2}$,QD=CD-CQ=1-$\frac{1}{2}$=$\frac{1}{2}$,
∴AM=QD,
又∵AM∥QD,
∴四邊形MAQD是平行四邊形.
(4)存在某一時刻t,使AO:OC=$\sqrt{2}$:1,理由如下:
如圖2,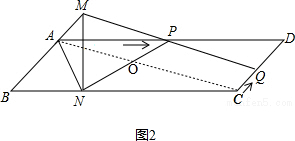
∵∠MNB=90°,∠B=45°,
∴△BMN是等腰直角三角形,
∴BN=MN=$\frac{\sqrt{2}}{2}$(t+1),
∵AD∥BC,
∴$\frac{AP}{CN}=\frac{AO}{OC}$,
∴$\frac{3t}{3-\frac{\sqrt{2}}{2}(t+1)}=\sqrt{2}$,
解得t=$\frac{3\sqrt{2}-1}{4}$,
∴存在t=$\frac{3\sqrt{2}-1}{4}$時,AO:OC=$\sqrt{2}$:1.
故答案為:t、$\frac{\sqrt{2}}{2}(t+1)$.
點評 (1)此題主要考查了四邊形綜合題,考查了分析推理能力,考查了數(shù)形結(jié)合思想的應用,要熟練掌握.
(2)此題還考查了平行四邊形的判定和性質(zhì)的應用,以及三角形的面積的求法,要熟練掌握.
(3)此題還考查了平行線的性質(zhì)和應用,要熟練掌握,解答此題的關(guān)鍵是要明確:①定理1:兩條平行線被第三條直線所截,同位角相等.簡單說成:兩直線平行,同位角相等.②定理2:兩條平行線被地三條直線所截,同旁內(nèi)角互補.簡單說成:兩直線平行,同旁內(nèi)角互補.③定理3:兩條平行線被第三條直線所截,內(nèi)錯角相等.簡單說成:兩直線平行,內(nèi)錯角相等.


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
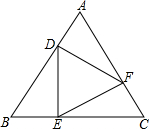 如圖,在等邊△ABC中,D、E、F三點分別在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,F(xiàn)D⊥AB于D.
如圖,在等邊△ABC中,D、E、F三點分別在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,F(xiàn)D⊥AB于D.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
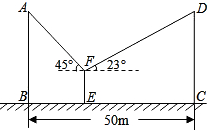 已知相鄰的兩根電線桿AB與CD高度相同,且相距BC=50m.小王為測量電線桿的高度,在兩根電線桿之間某一處E架起測角儀,如圖所示,分別測得兩根電線桿頂端的仰角為45°、23°,已知測角儀EF高1.5m,則電線桿的高度約為16.5m.(精確到0.1m,參考數(shù)據(jù):sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相鄰的兩根電線桿AB與CD高度相同,且相距BC=50m.小王為測量電線桿的高度,在兩根電線桿之間某一處E架起測角儀,如圖所示,分別測得兩根電線桿頂端的仰角為45°、23°,已知測角儀EF高1.5m,則電線桿的高度約為16.5m.(精確到0.1m,參考數(shù)據(jù):sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | 3 | D. | -1或1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com