【題目】某商場銷售某種品牌的手機,每部進貨價為2500元.市場調研表明：當銷售價為2900元時,平均每天能售出8部；而當銷售價每降低50元時,平均每天就能多售出4部.
（1）當售價為2800元時,這種手機平均每天的銷售利潤達到多少元?
（2）若設每部手機降低x元,每天的銷售利潤為y元,試寫出y與x之間的函數關系式．
（3）商場要想獲得最大利潤,每部手機的售價應訂為為多少元？此時的最大利潤是多少元？
【答案】（1）當售價為2800元時,這種手機平均每天的銷售利潤達到4800元；
（2）
；
（3）每臺彩電降價150元時,商場每天銷售這種彩電的利潤最大,最大利潤是5000元．
【解析】
試題（1）當售價為2800元時,銷售價降低100元,平均每天就能售出16部.即可求出每天利潤；
（2）根據：利潤=（每臺實際售價﹣每臺進價）×銷售量,每臺實際售價=2900﹣x,銷售量=8+4×
,列函數關系式；
（3）利用二次函數的頂點坐標公式,求函數的最大值．
試題解析：（1）當售價為2800元時,銷售價降低100元,平均每天就能售出16部.
所以：這種手機平均每天的銷售利潤為：
（元）；
（2）根據題意,得
,
即；
（3）對于,
當
時,
所以,每臺彩電降價150元時,商場每天銷售這種彩電的利潤最大,最大利潤是5000元．
沖刺100分單元優化練考卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，正方形
的對角線
和
相交于點
，正方形
的邊
交
于點
，
交
于點
.
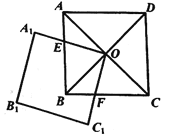
（1）求證：
；
（2）如果正方形的邊長為
，那么正方形繞點轉動的過程中，與正方形重疊部分的面積始終等于__________.（用含的代數式表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
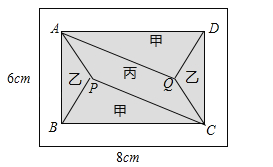
【題目】（2017浙江省溫州市）小黃準備給長8m，寬6m的長方形客廳鋪設瓷磚，現將其劃分成一個長方形ABCD區域Ⅰ（陰影部分）和一個環形區域Ⅱ（空白部分），其中區域Ⅰ用甲、乙、丙三種瓷磚鋪設，且滿足PQ∥AD，如圖所示．
（1）若區域Ⅰ的三種瓷磚均價為300元/m2，面積為S（m2），區域Ⅱ的瓷磚均價為200元/m2，且兩區域的瓷磚總價為不超過12000元，求S的最大值；
（2）若區域Ⅰ滿足BC=2：3，區域Ⅱ四周寬度相等．
①求AB，BC的長；
②若甲、丙兩瓷磚單價之和為300元/m2，乙、丙瓷磚單價之比為5：3，且區域Ⅰ的三種瓷磚總價為4800元，求丙瓷磚單價的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
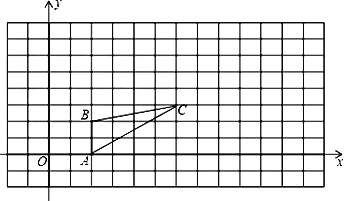
【題目】如圖，圖中的小方格都是邊長為1的正方形，△ABC的A、B、C三點坐標為A（2,0）、B（2,2）、C（6，3）。
（1） 請在圖中畫出一個△
,使△與△ABC是以坐標原點為位似中心，相似比為2的位似圖形。
（2）求△的面積。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以正方形的中心O為頂點作一個直角，直角的兩邊分別交正方形的兩邊BC、DC于E、F點，問：
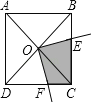
（1）△BOE與△COF有什么關系？證明你的結論（提示：正方形的對角線把正方形分成全等的四個等腰直角三角形，即正方形的對角線垂直相等且相互平分）；
（2）若正方形的邊長為2，四邊形EOFC的面積為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
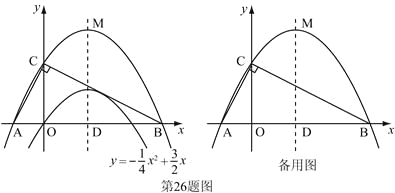
【題目】（本題滿分12分）已知二次函數
的圖象如圖.
（1）求它的對稱軸與
軸交點D的坐標；
（2）將該拋物線沿它的對稱軸向上平移，設平移后的拋物線與軸，
軸的交點分別為A、B、C三點，若∠ACB=90°，求此時拋物線的解析式；
（3）設（2）中平移后的拋物線的頂點為M，以AB為直徑，D為圓心作⊙D，試判斷直線CM與⊙D的位置關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
中，
，
的頂點
是底邊
的中點，兩邊分別與
交于點
．
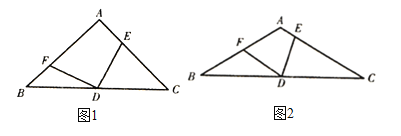
（1）如圖1，
，當
的位置變化時，
是否隨之變化？證明你的結論；
（2）如圖2，當
，當
°時，（1）中的結論仍然成立，求出此時的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
