
【題目】如圖,四邊形ABCD內接于⊙O,AB=AC,BD⊥AC,垂足為E,點F在BD的延長線上,且DF=DC,連接AF、CF.
(1)求證:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
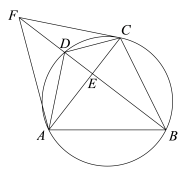
【答案】(1)見解析;(2) tan∠BAD=![]() .
.
【解析】
(1)根據等腰三角形的性質得出∠ABC=∠ACB,根據圓心角、弧、弦的關系得到![]() =
=![]() ,即可得到∠ABC=∠ADB,根據三角形內角和定理得到∠ABC=
,即可得到∠ABC=∠ADB,根據三角形內角和定理得到∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,∠ADB=90°∠CAD,從而得到
∠BAC,∠ADB=90°∠CAD,從而得到![]() ∠BAC=∠CAD,即可證得結論;
∠BAC=∠CAD,即可證得結論;
(2)易證得BC=CF=4![]() ,即可證得AC垂直平分BF,證得AB=AF=10,根據勾股定理求得AE、CE、BE,根據相交弦定理求得DE,即可求得BD,然后根據三角形面積公式求得DH,進而求得AH,解直角三角形求得tan∠BAD的值.
,即可證得AC垂直平分BF,證得AB=AF=10,根據勾股定理求得AE、CE、BE,根據相交弦定理求得DE,即可求得BD,然后根據三角形面積公式求得DH,進而求得AH,解直角三角形求得tan∠BAD的值.
解:(1)∵AB=AC,
∴![]() =
=![]() ,∠ABC=∠ACB,
,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=![]() (180°∠BAC)=90°
(180°∠BAC)=90°![]() ∠BAC,
∠BAC,
∵BD⊥AC,
∴∠ADB=90°∠DAC,
∴![]() ∠BAC=∠DAC,
∠BAC=∠DAC,
∴∠BAC=2∠DAC;
(2)∵DF=DC,
∴∠BFC=![]() ∠BDC=
∠BDC=![]() ∠BAC=∠FBC,
∠BAC=∠FBC,
∴CB=CF,
又BD⊥AC,
∴AC是線段BF的中垂線,AB= AF=10, AC=10.
又BC=4![]() ,
,
設AE=x, CE=10-x,
AB2-AE2=BC2-CE2, 100-x2=80-(10-x)2, x=6
∴AE=6,BE=8,CE=4,
∴DE=![]() =
=![]() =3,
=3,
∴BD/span>=BE+DE=3+8=11,
作DH⊥AB,垂足為H,
∵![]() ABDH=
ABDH=![]() BDAE,
BDAE,
∴DH=![]() ,
,
∴BH=![]() ,
,
∴AH=ABBH=10![]() ,
,
∴tan∠BAD=![]() =
=![]() =
=![]() .
.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
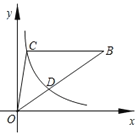
【題目】如圖,△OBC的邊BC∥x軸,過點C的雙曲線y=![]() (k≠0)與△OBC的邊OB交于點D,且OD:DB=1:2,若△OBC的面積等于8,則k的值為__.
(k≠0)與△OBC的邊OB交于點D,且OD:DB=1:2,若△OBC的面積等于8,則k的值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在菱形ABCD中,AB=4,∠BAD=120°,點P是直線AB上任意一點,聯結PC,在∠PCD內部作射線CQ與對角線BD交于點Q(與B、D不重合),且∠PCQ=30°.
(1)如圖,當點P在邊AB上時,如果BP=3,求線段PC的長;
(2)當點P在射線BA上時,設![]() ,求y關于
,求y關于![]() 的函數解析式及定義域;
的函數解析式及定義域;
(3)聯結PQ,直線PQ與直線BC交于點E,如果![]() 與
與![]() 相似,求線段BP的長.
相似,求線段BP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 的圖象經過坐標原點
的圖象經過坐標原點![]() ,且與
,且與![]() 軸另交點為
軸另交點為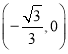 .
.
(1)求拋物線![]() 的解析式;
的解析式;
(2)如圖![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 相交于點
相交于點![]() 和點
和點![]() (點
(點![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
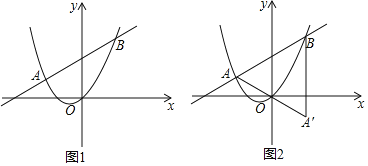
(3)在(2)中,若![]() ,設點
,設點![]() 是點
是點![]() 關于原點
關于原點![]() 的對稱點,如圖
的對稱點,如圖![]() .平面內是否存在點
.平面內是否存在點![]() ,使得以點
,使得以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,直接寫出點
為頂點的四邊形是菱形?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,D為AB的中點,以CD為直徑的⊙O分別交AC,BC于點E,F兩點,過點F作FG⊥AB于點G.
(1)試判斷FG與⊙O的位置關系,并說明理由.
(2)若AC=3,CD=2.5,求FG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,分別過點![]() ,
,![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 和
和![]() ,探究直線
,探究直線![]() 、
、![]() 與函數
與函數![]() 的圖象(雙曲線)之間的關系,下列結論正確的是( )
的圖象(雙曲線)之間的關系,下列結論正確的是( )
A.兩條直線可能都不與雙曲線相交
B.當![]() 時,兩條直線與雙曲線的交點到原點的距離不相等
時,兩條直線與雙曲線的交點到原點的距離不相等
C.當![]() 時,兩條直線與雙曲線的交點都在
時,兩條直線與雙曲線的交點都在![]() 軸左側
軸左側
D.當![]() 時,兩條直線與雙曲線的交點都在
時,兩條直線與雙曲線的交點都在![]() 軸右側
軸右側
查看答案和解析>>
科目:初中數學 來源: 題型:
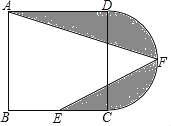
【題目】如圖,在正方形ABCD中,AB=12,點E為BC的中點,以CD為直徑作半圓CFD,點F為半圓的中點,連接AF,EF,圖中陰影部分的面積是_________。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com