
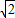 x-8與y軸交于P.
x-8與y軸交于P.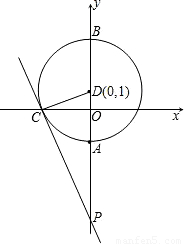
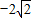 ,0),P(0,-8),根據cot∠OCD=
,0),P(0,-8),根據cot∠OCD= ,cot∠OPC=
,cot∠OPC=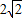 ,得∠OCD=∠OPC,∠OCD+∠PCO=90°,即PC是⊙D的切線;
,得∠OCD=∠OPC,∠OCD+∠PCO=90°,即PC是⊙D的切線; ×8×|x|,解得x=±
×8×|x|,解得x=±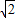 ,由y=-2
,由y=-2 x-8可知:當x=
x-8可知:當x=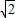 時,y=-12,當x=-
時,y=-12,當x=-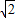 時,y=-4,所以在直線PC上存在點E(
時,y=-4,所以在直線PC上存在點E(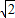 ,-12)或(-
,-12)或(-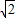 ,-4),
,-4),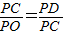 ,即PC2=PO•PD,可知PO•PD=PF•PQ,∠FPO=∠DPQ,從而證明△FPO∽△DPQ
,即PC2=PO•PD,可知PO•PD=PF•PQ,∠FPO=∠DPQ,從而證明△FPO∽△DPQ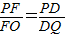 ,即
,即 ,即m=3n(2<n<
,即m=3n(2<n<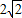 ).
).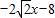 與x軸、y軸分別交于點C、P,
與x軸、y軸分別交于點C、P,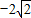 ,0),P(0,-8),
,0),P(0,-8),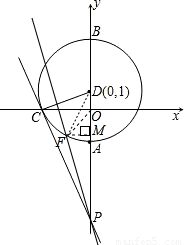
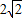 ,cot∠OPC=
,cot∠OPC=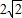 ,
, ×8×|x|=4×
×8×|x|=4× ×1×2
×1×2 ,
,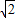 ,由y=-2
,由y=-2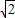 x-8可知:
x-8可知: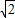 時,y=-12,
時,y=-12,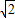 時,y=-4,
時,y=-4,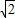 ,-12)或(-
,-12)或(-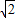 ,-4),
,-4),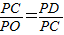 ,
,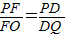 ,即
,即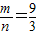 ,
,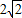 ).
).
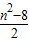 ②,
②,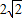 ).
).

 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:初中數學 來源: 題型:
| 3 |
| 3 |
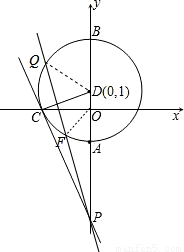
 ,D兩點.
,D兩點.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,拋物線交x軸于點A(-2,0),點B(4,0),交y軸于點C(0,4).
如圖,拋物線交x軸于點A(-2,0),點B(4,0),交y軸于點C(0,4).查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |
 P,且D的坐標(0,1).
P,且D的坐標(0,1).查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 3 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com