(本小題共l4分)
已知

函數
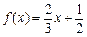
,
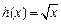
.
(Ⅰ)設函數
F(
x)=18
f(
x)-
x2[
h(
x)]
2,求
F(
x)的單調區間與極值;
(Ⅱ)設
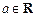
,解關于
x的方程
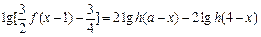
;
(Ⅲ)設
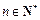
,證明:
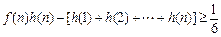
.
解:(Ⅰ)
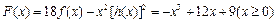
,
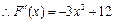
.
令
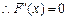
,得
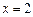
(
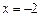
舍去).
當
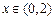
時.
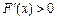
;當

時,
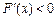
,
故當
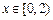
時,
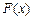
為增函數;當
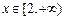
時,
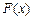
為減函數.
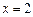
為
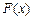
的極大值點,且
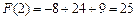
.
(Ⅱ)方法一:原方程可化為
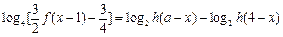
,
即為
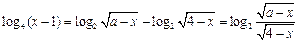
,且
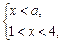
①當
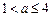
時,
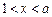
,則
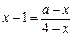
,即
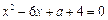
,
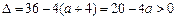
,此時
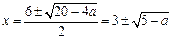
,∵
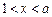
,
此時方程僅有一解
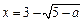
.
②當
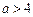
時,
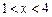
,由
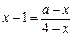
,得
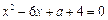
,
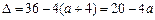
,
若
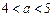
,則
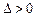
,方程有兩解
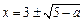
;
若
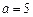
時,則

,方程有一解
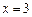
;
若
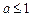
或
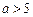
,原方程無解.
方法二:原方程可化為
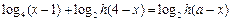
,
即
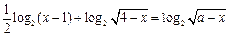
,
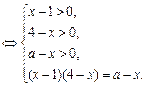
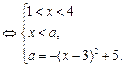
①當
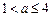
時,原方程有一解
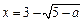
;
②當
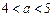
時,原方程有二解
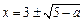
;
③當
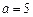
時,原方程有一解
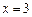
;
④當
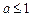
或
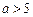
時,原方程無解.
(Ⅲ)由已知得
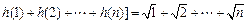
,
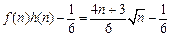
.
設數列
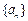
的前
n項和為
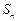
,且
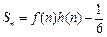
(
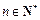
)
從而有
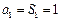
,當
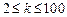
時,
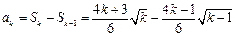
.
又
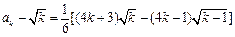
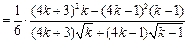
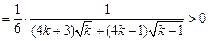
.
即對任意
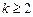
時,有
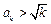
,又因為
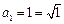
,所以
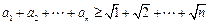
.
則
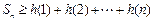
,故原不等式成立.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)已知
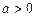
,設函數
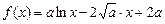
,
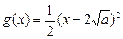
.
(Ⅰ)求函數
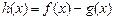
的最大值;
(Ⅱ)若
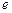
是自然對數的底數,當
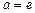
時,是否存在常數
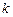
、
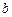
,使得不等式
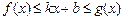
對于任意的正實數
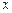
都成立?若存在,求出
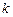
、
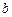
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知函數
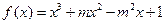
(m為常數,且m>0)有極大值9.
(1)求m的值;
(2)若斜率為-5的直線是曲線
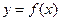
的切線,求此直線方程
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
函數
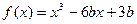
在(0,1)內有極小值,則實數
b的取值范圍是
| A.(0,1) | B.(-∞,1) |
| C.(0,+∞) | D.(0,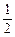 ) ) |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)
設
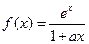
,其中
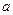
為正實數
(Ⅰ)當
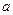
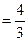
時,求
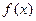
的極值點;
(Ⅱ)若
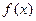
為
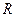
上的單調函數,求
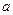
的取值范圍。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
曲線
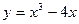
在點
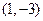
處的切線傾斜角為__________
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
曲線
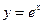
在點A(0,1)處的切線斜率為( )
| A.1 | B.2 | C.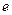 | D.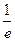 |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知直線
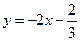
與曲線
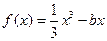
相切。
(1)求b的值;
(2)若方程
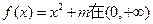
上有兩個解
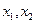
,求m的取值范圍。
查看答案和解析>>
主站蜘蛛池模板:
91久久精品国产91久久
|
女女野外嗯啊高潮h百合扶她
|
精品在线一区二区三区
|
夜夜骑天天射
|
黄色羞羞视频在线观看
|
蜜桃视频网站在线观看
|
国产成人综合在线
|
久久久久美女
|
国产区 在线观看
|
精品久久国产
|
国产在线视频网
|
欧美日韩影院
|
欧美日韩在线不卡
|
午夜精品一区二区三区免费视频
|
久久国产一区二区三区
|
久久二区三区
|
日韩精品在线一区
|
精品福利一区二区
|
欧美久久久久久
|
老司机深夜福利在线观看
|
久久这里只有精品首页
|
日本久久精品
|
国产一区二区三区在线视频
|
欧美福利一区二区
|
亚洲精品字幕
|
亚洲精品自拍视频
|
国产高清精品一区二区三区
|
欧美精品片
|
91福利在线导航
|
精品国产乱码久久久久久牛牛
|
久久亚洲精品中文字幕蜜潮电影
|
99久久婷婷国产精品综合
|
国产wwwcom|
亚洲精品一区二区网址
|
黄色成人在线
|
欧美日韩国产综合视频
|
欧美精品久久久久久久监狱
|
国产一区av在线
|
国产一区二区黄
|
国产精品久久久久久久久福交
|
亚洲天堂av中文字幕
|

 函數
函數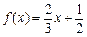 ,
,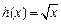 .
.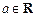 ,解關于x的方程
,解關于x的方程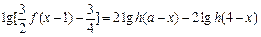 ;
;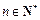 ,證明:
,證明: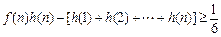 .
. 快樂5加2金卷系列答案
快樂5加2金卷系列答案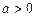 ,設函數
,設函數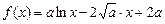 ,
,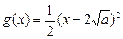 .
.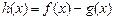 的最大值;
的最大值;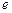 是自然對數的底數,當
是自然對數的底數,當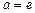 時,是否存在常數
時,是否存在常數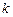 、
、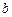 ,使得不等式
,使得不等式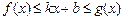 對于任意的正實數
對于任意的正實數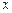 都成立?若存在,求出
都成立?若存在,求出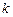 、
、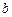 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.