40.2
分析:算式①可根據加法與減法、乘法與除法的互逆關系計算;
算式②可將式中的乘法算式分解為具有共同因數3×6的算式后再根據乘法分配律計算;
算式③可將原式分解為1-

+1-

-(1-

)+1-

-(1-

)進行計算;
算式④可根據等式的性質進行解方程:方程的兩邊同時加上、減去、乘以、或除以同一個數,等式仍然成立;
算式⑤可根據除以一個數等于乘以這個數的倒數的計算法則,將除法算式化為乘法算式后通過約分計算,即原式=1×

×

×

×…
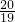
;
算式⑥可根據乘法分配律進行計算.
解答:①6030÷(4050-3900)
=6030÷150,
=40.2;
所以4050-6030÷40.2=3900;
②3×6+33×66+333×666
=3×6+11×3×11×6+111×3×111×6,
=(1+11×11+111×111)×3×6,
=12443×18,
=223974;
③1-

+

-

+

-

=1-

+1-

-(1-

)+1-

-(1-

)
=1-

+1-

-1+

+1-

-1+

,
=

-

+

-

+

,
=

;
④10.1-17X=1.86-15
10.1-17X+15=1.86-15+15
25.1-17X=1.86
25.1-17X+17X=1.86+17X
25.1-1.86=1.86+17X-1.86
23.24=17X
X=

;
⑤1÷(2÷3)÷(3÷4)÷(4÷5)÷…÷(19÷20)
=1
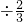
÷

÷…

,
=1×

×

×

×…
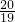
,
=10;
⑥3

×(3
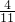
+
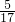
)+3.4×

=

×
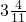
+

×
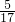
+

×

,
=(
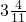
+

)×

+1,
=4×

+1,
=13.6+1,
=14.6.
點評:本題式中數據較為復雜,完成時要細心,運用合適的方法進行計算.

 +
+ -
- +
+ -
- =
= ×(3
×(3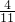 +
+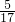 )+3.4×
)+3.4× =
= +1-
+1- -(1-
-(1- )+1-
)+1- -(1-
-(1- )進行計算;
)進行計算; ×
× ×
× ×…
×…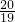 ;
; +
+ -
- +
+ -
-
 +1-
+1- -(1-
-(1- )+1-
)+1- -(1-
-(1- )
) +1-
+1- -1+
-1+ +1-
+1- -1+
-1+ ,
, -
- +
+ -
- +
+ ,
, ;
; ;
;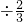 ÷
÷ ÷…
÷… ,
, ×
× ×
× ×…
×…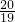 ,
, ×(3
×(3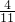 +
+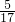 )+3.4×
)+3.4×
 ×
×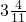 +
+ ×
×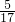 +
+ ×
× ,
,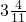 +
+ )×
)× +1,
+1, +1,
+1,
