已知三個圓的半徑都是3厘米,求陰影部分的面積.
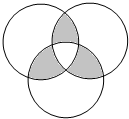
考點:組合圖形的面積
專題:平面圖形的認(rèn)識與計算
分析:如圖所示,連接其中一個陰影部分的三點構(gòu)成一個等邊三角形,從圖中你會發(fā)現(xiàn):每一塊陰影部分面積=正三角形面積+兩個弓形面積-一個弓形面積=扇形面積.所以我們可以求出以這個以這個小陰影部分為主的扇形面積=
cm
2,再乘3,就是陰影的總面積.
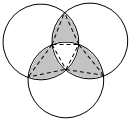
解答:
解:3
2=9
由題意,得:
S
陰影=3×S
扇形,
=3×
=3×
π
=4.5π
=14.13(cm
2).
答:陰影部分的面積是14.13平方厘米.
點評:本題的關(guān)鍵是看出每一塊陰影部分面積=正三角形面積+兩個弓形面積-一個弓形面積,即一個圓心角為60°的扇形的面積.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:小學(xué)數(shù)學(xué)
來源:
題型:
小剛有郵票25張.淘氣的郵票是小剛的3倍;笑笑的郵票是小剛的2倍少17張.
(1)淘氣和笑笑各收藏了多少張的郵票?
(2)笑笑和小剛共收藏了多少張的郵票?
(3)你還能提出什么數(shù)學(xué)問題?并試著解答.
查看答案和解析>>
科目:小學(xué)數(shù)學(xué)
來源:
題型:
一個數(shù)的40%等于100,這個數(shù)的
是多少?
查看答案和解析>>
科目:小學(xué)數(shù)學(xué)
來源:
題型:
在等腰直角三角形中,如下圖,求陰影部分面積.
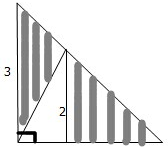
查看答案和解析>>
科目:小學(xué)數(shù)學(xué)
來源:
題型:
如圖,AO=BO=4cm,求陰影部分的面積.
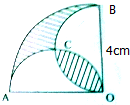
查看答案和解析>>
科目:小學(xué)數(shù)學(xué)
來源:
題型:
先看一看第一行的數(shù)怎樣得到第二行的數(shù),再把表填完全.
| 13 | 100 | 25 | 31 | 205 | 720 | 315 | 0 |
| 52 | 400 | 100 | | | | | |
查看答案和解析>>




