Question

2．只用下面一種圖形可以進行密鋪的有（　　）

• A．
• B．
• C．
• D．

Answer 1

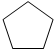分析 幾何圖形鑲嵌成平面的關鍵是：圍繞一點拼在一起的多邊形的角加在一起恰好組成一個周角．根據密鋪的知識可得圓和正五邊形不能單獨密鋪，然后找到內角和能整除360°的多邊形和一個角能整除周角360°的正多邊形即可．

解答 解：圓不能進行單獨密鋪，不符合題意；
長方形的每個角是90°，4個角能組面一個周角，能密鋪；
由于三角形的角和是180°，幾個角能組成一個周角，能密鋪．
正五邊形每個角是180°-360°÷5=108°，5個角不能組成一個周角，不能密鋪；
故選：B，C．

點評 本題考查平面密鋪的知識，注意掌握只用一種正多邊形鑲嵌，只有正三角形，正四邊形，正六邊形三種正多邊形能鑲嵌成一個平面圖案．任意多邊形能進行鑲嵌，說明它的內角和應能整除360°．