Question

8．按要求在方格紙上畫圖（每個小方格表示1平方厘米）．
①先用數對表示圖中A點的位置是（4，5）；再把圖中的三角形繞A點順時針旋轉90°．
②按1：2的比畫出圓縮小后的圖形．縮小后的圓形面積是原來的$\frac{（）}{（）}$．
③在方格紙上畫一個面積是8平方厘米的軸對稱圖形，并畫出1條對稱軸．

Answer 1

分析 （1）①數對表示位置的方法是：第一個數字表示列，第二個數字表示行；
②繞A點旋轉時，先把AB和AC兩邊，繞點A順時針旋轉90°，得到旋轉后的直角三角形的兩條直角邊，由此即可確定旋轉后的三角形的位置與大小；
（2）按1：2的比畫出圓縮小后的圖形，是指把圓的半徑縮小2倍，根據圓的面積公式可得：縮小后的圓形面積與原來的圓的面積之比是1：4，由此即可解決問題．
（3）可以畫一個長為4厘米，寬為2厘米的長方形，并畫出它的一條對稱軸．

解答 解：（1）根據數對表示位置的方法可得：點A的位置為：（4，5），根據圖形旋轉的性質可得出三角形ABC旋轉后的圖形M，如下圖所示；
（2）根據圖形縮小的性質，抓住圓的半徑縮小2倍，可以得出縮小后的圓形如下圖所示，根據圓的面積公式可得：縮小后的圓形面積是原來的$\frac{1}{4}$；
（3）長方形是軸對稱圖形，由此可以畫出這個面積是8平方厘米的長方形，如圖所示：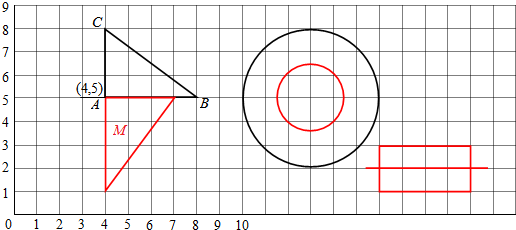

故答案為：（1）（4，5）；（2）$\frac{1}{4}$．

點評 （1）此題考查了數對表示位置的方法以及圖形的旋轉的性質；
（2）考查了圓的放大與縮小的性質，這里要抓住圓的半徑進行畫圖；
（3）考查了軸對稱圖形的特點以及對稱軸的確定方法．