分析:首先考慮通過三角形中BE,AD,CF線段組成的圖形內三角形的個數,然后連接EF,再次計算連接EF后增加的三角形的數量,再連接DF,計算連接DF后增加的三角形的數量,接著連接DE,計算連接DE后增加的三角形的數量,最后把這些三角形數量相加即可得到答案.
解答:解:首先考慮圖1三角形的個數,
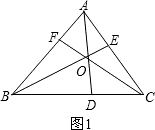
三角形有:△AFO,△AFC,BFO,△BFC,△ABO,△BDO,△BDA,△CDO,△CDA,△BCO,△CEO,△CEB,△AEO.AEB,△ACO,△ABC共16個三角形,
連接EF后如圖2,三角形有:△AGE,△AGF,△FGO,△GOE,△EFB,△EFA,△EFC,△EFO共8個,
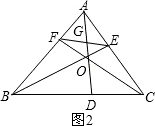
連接DF后,如圖3,三角形有:△BFH,△FOH,△BHD,△HOD,△FOE,△BDF,△DFG,△FDC,共8個,
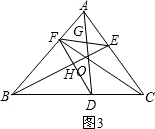
連接DE后,如圖4,三角形有:△EIC、△DIC、△EIC、△OID、△OEC、△ODC、△EIF、△IFD、△ADE、△DEF、△BDE、△DCE,共12個,
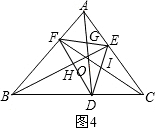
綜上共有三角形16+8+8+12=44個.
答:一共有44個三角形.
點評:本題主要考查計數方法的知識點,解答本題的關鍵是掌握計數原理和不在同一直線上的三點可以構成一個三角形.








 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案