Question

求圖中陰影部分的面積（第2小題要求圖形的周長）．
（1）                             （2）

Answer 1

考點：組合圖形的面積

專題：平面圖形的認識與計算

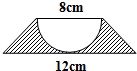
分析：（1）陰影部分的面積=梯形的面積-半圓的面積；圓的半徑為：（8÷2）厘米；梯形的高等于圓的半徑，根據梯形、圓的面積公式解答即可．
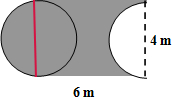
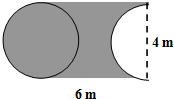
（2）把左邊的半圓割補到右邊空白半圓處，則陰影部分的面積=長方形的面積（長為6米、寬為4米）；
陰影部分的周長=直徑為4米的圓的周長+兩條長為6米的邊；根據圓的周長公式：C=πd，解答即可．

解答： 解：（1）（8+12）×（8÷2）×2-3.14×（8÷2）²÷2 
=40-25.12
=14.88（平方厘米）
答：陰影部分的面積是14.88平方厘米．

（2）陰影部分的面積：
6×4=24（平方米）
陰影部分的周長：
3.14×4+6×2
=12.56+12
=24.56（米）
答：陰影部分的面積是24平方米；周長為24.56米．

點評：（1）此題考查組合圖形面積的計算方法，一般都是轉化到規則圖形中利用面積公式計算解答．
（2）分析圖形，根據圖形特點進行割補，尋求問題突破點．