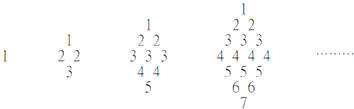100
分析:第一個圖中,數字是1,
第二個圖中,數字之和可以分成2部分(1+2)+(2+3)=3+5=8;兩部分的和相差2;所以第二幅圖中數字之和可以寫成(1+2)×2+1×2=8;
第三幅圖中,數字之和可以分成三部分:(1+2+3)+(2+3+4)+(3+4+5)=6+9+12,三部分和之間依次相差3,所以第三幅圖中的數字之和可以寫成:(1+2+3)×3+(1+2)×3=27;
第四幅圖中,數字之和可以分成四部分:(1+2+3+4)+(2+3+4+5)+(3+4+5+6)+(4+5+6+7)=10+14+18+22,四部分之間依次相差4,所以第四幅圖中的數字之和可以寫成:(1+2+3+4)×4+(1+2+3)×4=64;…
所以第n個圖形的數字之和就是:(1+2+3+…+n)×n+(1+2+3+…+n-1)×n,由此即可解決問題.
解答:根據題干分析可得:第n個圖形的數字之和就是:(1+2+3+…+n)×n+(1+2+3+…+n-1)×n,
當n=100時,數字之和是:
(1+2+3+…+100)×100+(1+2+3+…+99)×100,
=5050×100+4950×100,
=505000+495000,
=1000000,
第 100 個圖內所有數字的總和為1000000.
故答案為:1000000.
點評:主要考查了學生通過特例分析從而歸納總結出一般結論的能力.對于找規律的題目首先應找出哪些部分發生了變化,是按照什么規律變化的,通過分析找到各部分的變化規律后直接利用規律求解.