Question

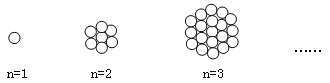
【題目】如圖，當n=1時，圖中有1個圓；當n=2時，圖中有7個圓；當n=3時，圖中有19個圓；…，按此規律，當n=5時，圖中有 個圓．

Answer 1

【答案】61

【解析】所構成的圖形是軸對稱圖形，沿中間的一列分開，兩邊對稱，最左邊的一行是n個圓，后面每一列比前面的每一列多一個，直到中間的一列，中間的一排是2n﹣1個．中間的后面的每排依次減少．

解：最左邊的一列是n，第二列是n+1，第三列是n+2，…，第n列是2n﹣1；

第n列以后，各列的個數分別是2n﹣2，2n﹣3…，n．

則第n個圖形的圓的個數是：

n+（n+1）+…（2n﹣1）+（2n﹣2）+（2n﹣3）+…+n

=2[n+（n+1）+（n+2）+…+（2n﹣2）]+（2n﹣1）

=（n﹣1）[n+（2n﹣2）]+（2n﹣1）

=3n2﹣3n+1．

所以當n=5時，圖中有圓：3×52﹣3×5+1，

=3×25﹣15+1，

=75﹣15+1，

=61（個），

答：當n=5時，圖中有圓61個．

故答案是：61．