分析:幾何圖形鑲嵌成平面的關鍵是:圍繞一點拼在一起的多邊形的內角加在一起恰好組成一個周角.360°為正多邊形一個內角的整數倍才能單獨鑲嵌.任意一種多邊形能進行鑲嵌,說明它的內角和應能整除360°.
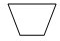
解答:解:梯形的內角和是360°,放在同一頂點處4個即能密鋪;
任意三角形的內角和是180°,放在同一頂點處6個即能密鋪;
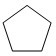
正五邊形每個內角是180°-360°÷5=108°,不能整除360°,不能密鋪;
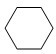
正六邊形的每個內角是120°,能整除360°,能密鋪;
故選:D.
點評:考查了平面鑲嵌(密鋪)問題,兩種或兩種以上幾何圖形鑲嵌成平面的關鍵是:圍繞一點拼在一起的多邊形的內角加在一起恰好組成一個周角.