����⣺
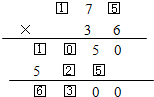
��1���ɂ���(sh��)��λ�ϵĔ�(sh��)��˵�ĩβ��0����5��6=30���ɵã���һ����(sh��)��λ�ϵĔ�(sh��)��5��
��һ����(sh��)��75�cʮλ�ϵ�3��˵ķe��5������ֻ��175��3=525���ɵõ�һ����(sh��)��λ�ϵĔ�(sh��)��1������һ����(sh��)��175��
�����Ͽɵã�
��
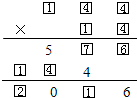
��2����һ����(sh��)��λ�ϵĔ�(sh��)�c�ڶ�����(sh��)��λ�ϵĔ�(sh��)��˵ķe��ĩβ��6��������һ����(sh��)�c�ڶ�����(sh��)��λ�ϵĔ�(sh��)��˵ķe��5��������ô�ڶ�����(sh��)��λ�ϵĔ�(sh��)�����^5��
���O(sh��)�ڶ�����(sh��)��λ�ϵĔ�(sh��)��1����ô��λ�ϵĔ�(sh��)��5����˵ķe������5������1��6=6����һ����(sh��)��λ�ϵĔ�(sh��)��6����һ����(sh��)��λ�ϵĔ�(sh��)6�c�ڶ�����(sh��)ʮλ�ϵĔ�(sh��)��˵ķe��ĩβ��4��6��4=24��6��9=54����Փ�ڶ�����(sh��)ʮλ�ϵĔ�(sh��)��4��߀��9���c��ٶ�������õķe������λ��(sh��)���������}�⣻
���O(sh��)�ڶ�����(sh��)��λ�ϵĔ�(sh��)��2����ô��λ�ϵĔ�(sh��)��2����˵ķe������5�������@�r��һ����(sh��)ʮλ�ϵĔ�(sh��)���ڻ����5��2��3=6��2��8=16����һ����(sh��)��λ�ϵĔ�(sh��)��3��8����(d��ng)?sh��)�һ����(sh��)��λ�ϵĔ�(sh��)��3�r��3��8=24��8�c���ٶ���˵ķe����λ��(sh��)�������ϣ���(d��ng)?sh��)�һ����(sh��)��λ�ϵĔ�(sh��)��8�r��8��3=24��8��8=64��ֻ��3�˶��ٶ���˵ķe����λ��(sh��)�����Եڶ�����(sh��)ʮλ�ϵĔ�(sh��)��3�����ڶ�����(sh��)��32��258��32=8256��268��32=8576��278��32=8896��288��32=9216��298��32=9536�������ϣ���˵ڶ�����(sh��)��λ�ϵĔ�(sh��)��2�����ϣ�
���O(sh��)�ڶ�����(sh��)��λ�ϵĔ�(sh��)��3��3��2=6����һ����(sh��)��λ�ϵĔ�(sh��)��2��2��2=4��2��7=14���ڶ�����(sh��)ʮλ�ϵĔ�(sh��)��2��7�����ڶ�����(sh��)��23��73�������ֻ�е�һ����(sh��)��172��182��192�r����һ����(sh��)�c3�������ٶࣻ172��182��192�c7��˶�����λ��(sh��)�����ԣ��ڶ�����(sh��)��23��172��23=3956��182��23=4186��192��23=4416�������ϣ���˵ڶ�����(sh��)��λ�ϵĔ�(sh��)��3�����ϣ�
���O(sh��)�ڶ�����(sh��)��λ�ϵĔ�(sh��)��4��4��4=16��4��9=36����(d��ng)?sh��)�һ����(sh��)��λ�ϵĔ�(sh��)��4�r��4��1=4��4��6=24���ڶ�����(sh��)ʮλ�ϵĔ�(sh��)��1��6�����ڶ�����(sh��)��14��64����(d��ng)?sh��)�һ����(sh��)��λ�ϵĔ�(sh��)��9�r��9��6=54���ڶ�����(sh��)ʮλ�ϵĔ�(sh��)��6�����ڶ�����(sh��)��64����(j��ng)��C��ֻ��144��14=2016�����}�⣻
�����Ͽɵã�
��

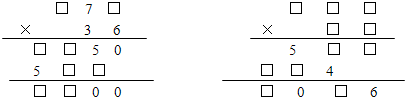
 ��
�� ��
��

 һ�����}�����}��ϵ�д�
һ�����}�����}��ϵ�д�
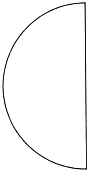 ��D��һ����A���������ÈAҎ(gu��)���@���A�������ԇһԇ������������A�����L��
��D��һ����A���������ÈAҎ(gu��)���@���A�������ԇһԇ������������A�����L��